这学期本来打算修一门计算复杂性的课，结果第一节课没选上没听导致第二节课想试听但是完全听不懂遂退了
2 Likes
这里和水源同步更新吧
如何构造 3 个同分布且总和为恒定常数的随机变量？
虽然有 3 个变量，但确定其二后另一个唯一确定，所以只有两个自由度。所以问题的关键在于如何让第三个变量也和前两个服从相同分布。
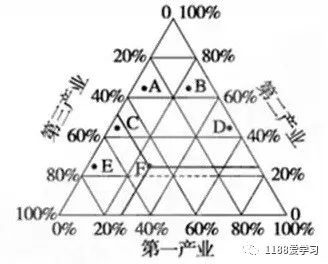
这让我想到高中地理常用的三角坐标系：二维平面内任意一点具有两个自由度，同时对应等边三角形三条边上的三个坐标。这三个坐标地位均等，所以如果分布对三角形均匀，例如三角形内的均匀分布或者平面内的正态分布，就一定能做到三个坐标同分布。
这个问题还可以推广到更高维的情况，关键在于把 (n-1) 维映射到 n 维。
这个问题的背景源自我的头像，我想让头像每一条线的亮度（RGB 三个值的总和）保持不变，但颜色随机变化，即 RGB 的每个值都在 0~255 之间随机变化。我原打算先给 R 生成
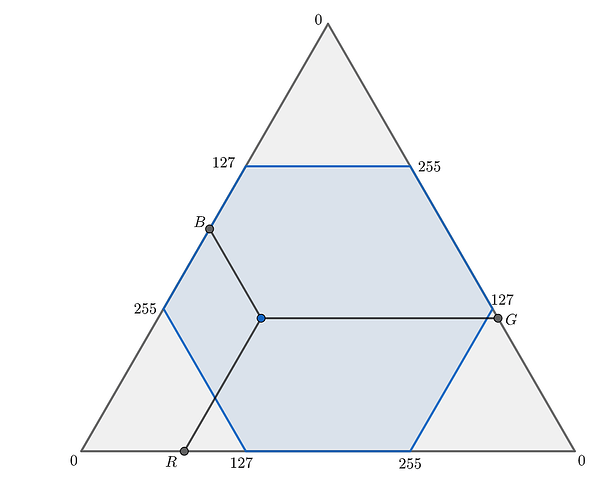
(0,255)的随机值，再给 G 生成(max(0,127-r),min(381-r,255)) 的随机值，最后得到 B，后来意识到这种方法生成的三个变量不满足同分布。如果按照三角坐标系的思路，为了让每个值的范围是 0~255，且平均值处于 127，其中一种方法是把上图正三角形挖去三个角，形成一个正六边形，然后在正六边形中均匀取点，得到三个对应的坐标，如下图。
当然在工程上还有更简单的处理方法，比如按最初方法生成完三个不同分布的随机数后随机交换位置，使之与 RGB 的对应关系也随机。如此同样可以实现最终的同分布。
原代码来自知乎文章 Python 画各种有趣的图及源码。我改变了线条的长度、粗细和颜色。
代码
# -*- coding: utf-8 -*-
from turtle import *
import random
length = 10
angle = 90
setup(1280,720)
up()
goto(-640,-360)
down()
def draw_path(path):
for symbol in path:
if symbol == 'f':
colormode(255)
color(random.randint(0,255),random.randint(0,255),random.randint(0,255))
fd(length)
elif symbol == '+':
lt(angle)
elif symbol == '-':
rt(angle)
def apply_path(rules,path):
lit = [x for x in path]
for i in range(len(lit)):
symbol = lit[i]
if symbol == 'x':
lit[i] = rules[symbol]
elif symbol == 'y':
lit[i] = rules[symbol]
path = ''.join(lit)
return path
rules = {
'x':'+yf-xfx-fy+',
'y':'-xf+yfy+fx-'
}
path = 'x'
speed(0)
for i in range(7):
path = apply_path(rules,path)
draw_path(path)
done()
3 Likes
如果函数 L:\mathbb{R}^n\to\mathbb{R} 满足如下条件：
- \boldsymbol{v}\mapsto L(\boldsymbol{v}) 是凸函数
- \displaystyle\lim_{|\boldsymbol{v}|\to \infty}\frac{L(\boldsymbol{v})}{|\boldsymbol{{v}}|}=\infty （超线性）
则 L 的 Legendre 变换为
L^*(\boldsymbol{p})=\sup_{\boldsymbol{v}\in\mathbb{R}^n}\{\boldsymbol{p}\cdot \boldsymbol{v}-L(\boldsymbol{v})\},\boldsymbol{p}\in\mathbb{R}^n.
Legendre 变换具有如下性质：
- \boldsymbol{p}\mapsto L^*(\boldsymbol{p}) 是凸函数
- \displaystyle\lim_{|\boldsymbol{p}|\to \infty}\frac{L^*(\boldsymbol{p})}{|\boldsymbol{p}|}=\infty （超线性）
- L^{**}=L
在理论力学中常见的 Legendre 变换是
L^*(\boldsymbol{p})=\boldsymbol{p}\cdot \boldsymbol{v}-L(\boldsymbol{v}),
其中
\boldsymbol{p}=\nabla L.
如果函数 L 可导，则两种定义是等价的。
3 Likes
好诶！
1 Like
基于 Markov 链的解决方法：
若要生成 n 个均匀分布的随机非负整数，且和为定值，则可以先任取一组满足和条件的数，然后每次随机选择两个数，对其中一个数 +1，另一个数 -1，除非另一个数已经达到 0。重复足够多次后，每个数可以近似为均匀分布，且和始终不变。
证明：每个数的转移矩阵为
\left( \begin{matrix}
\frac{n-1}{n}& \frac{1}{n}& 0& \cdots\\
\frac{1}{n}& \frac{n-2}{n}& \frac{1}{n}& \cdots\\
0& \frac{1}{n}& \frac{n-2}{n}& \cdots\\
\cdots& \cdots& \cdots& \cdots\\
\end{matrix} \right)
根据 Basic Limit Theorem，显然存在均匀的稳态分布，所以分布会趋于均匀。因为加减同时进行，所以所有数的和不变。
该方法还可以扩展到矩阵各行列之和固定的情形，只需每次既选择行，又选择列进行加减。
使用 Minecraft 进行蒙特卡洛模拟
3 Likes
看其它内容时经常用到张量，这几篇文章可以补一下基础
4 Likes
随机测度
设 (\Omega, \mathcal{F}, P) 是一个概率空间， (Z, \mathcal{B}_Z) 是一个可测空间（其中 \mathcal{B}_Z 是 Z 上的 σ-代数）. 一个随机测度 \mu 是一个映射：
\mu: \Omega \times \mathcal{B}_Z \to [0, \infty]
需要满足以下条件：
-
对于每个 B \in \mathcal{B} ， \mu(\cdot, B) 是一个随机变量，但可以取到 [0, \infty] ;
-
对于每个确定的 \omega \in \Omega ， \mu(\omega, \cdot) 是 (Z, \mathcal{B}_Z) 上一个σ-有限的测度（这里的σ-有限指存在 \{U_n\}_{n=1}^\infty\subset\mathcal{B}_Z 使得 Z=\cup_{n=0}^\infty U_n 并且 \mu (U_n,\omega) < \infty, \forall n ） .
Poisson 随机测度
一个取值为非负整数（包括无穷大）的随机测度 \mu(\omega,B) 如果满足以下条件，则为 Poisson 随机测度：
- 对每一个 B \in \mathcal{B} ， \mu(\cdot, B) 满足参数为 \lambda(B)=\mathbb{E}[ \mu(\omega,B)] 的 Poisson 分布，即 \mathbb{P}(\{\omega:\mu(\omega,B)=n\})=e^{-\lambda(B)}\frac{\lambda(B)^n}{n!},n=0,1,\cdots ;
- 如果 \{B_j\}_{j=1}^m\subset \mathcal{B}_Z 彼此不相交，那么 \{\mu(\cdot, B_j)\}_{j=1}^m 彼此独立.
如果在空间 Z 中随机撒点，那么对空间中一片确定的区域而言，这片区域的点数服从 Poisson 分布；对一次确定的撒点结果而言，空间中不同区域的点数是一个取值为非负整数的测度。所以点数就是一个 Poisson 随机测度。这里的空间中还可以包含时间，例如对 Z=\mathbb{R}_+\times \mathbb{R}^d ， \mu: \Omega \times \mathcal{B}_Z \to\mathbb{N}\cup\{\infty\} 就可以理解为每时每刻都有一定概率在 d 维欧氏空间中随机撒点，点数是一个 Poisson 随机测度。
2 Likes
在上次约饭时，@anon60541984 提出了头发生长与掉落速度恒定的假设，这里计算头发平均长度从 0 开始逐渐生长，并达到动态平衡的过程。
设头发的总数为 N ，每根头发在单位时间内增长 \iota ，且单位时间内有 n 根头发脱落和生长。
若 t 时刻的头发平均长度为 l(t) ，则在 \left( t+\Delta t \right) 时刻有
l\left( t+\Delta t \right) =\left( l\left( t \right) +\iota \Delta t \right) \left( 1-\frac{n\Delta t}{N} \right)
令 \Delta t\to 0 ，得到一阶常系数微分方程
\frac{dl}{dt}+\frac{n}{N}l-\iota =0
设 l(0)=0 ，则
l=\frac{\iota N}{n}\left( 1-\mathrm{e}^{-\frac{n}{N}t} \right)
头发平均长度最初的增加速度近似等于每根头发生长的速度，在时间足够长后达到稳定值 \frac{\iota N}{n} ，这也与物理直觉相符。
2 Likes
对这题，我出于对平面几何的朴素认识决定用微积分算。
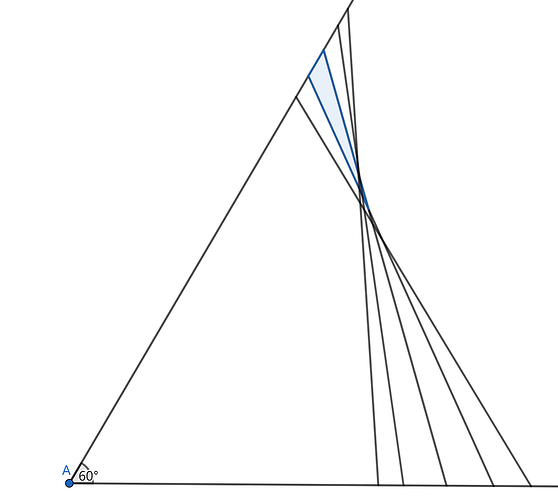
首先，这个运动过程前后对称，所以只需要研究木棍从紧贴上沿运动到与墙角形成等边三角形的过程。
其次，木棍从紧贴上沿到运动到与下沿垂直的过程中，扫过的图形显然为直角三角形，这部分很容易求解，所以只需要计算从直角三角形到等边三角形过程中扫过的不规则图形面积。
在这里，我把不规则图形拆成从上到下的一个个三角形（见蓝色部分），彼此不重合。所以只需要计算每个三角形的面积再积分。
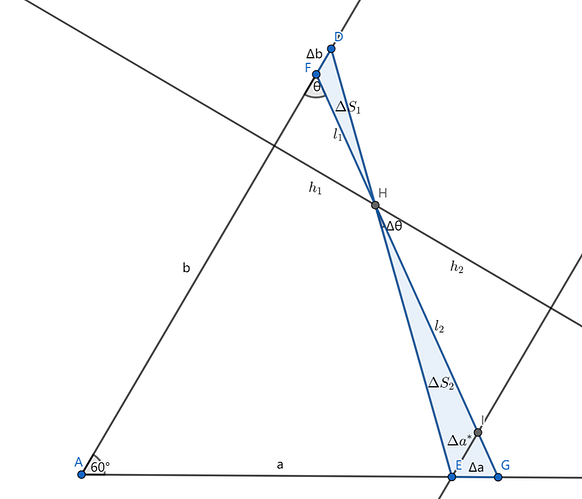
如何计算三角形的面积呢？如下图，我们首先规定木棍的长度为 l ，相对上沿的夹角为 \theta ，那么根据 \bigtriangleup DAE 的正弦定理，另外两条边的长度满足
\frac{a}{\sin \theta}=\frac{b}{\sin \left( \theta +\frac{\pi}{3} \right)}=\frac{l}{\sin \frac{\pi}{3}}
解得 a=\frac{2}{\sqrt{3}}l\sin \theta ,b=\frac{2}{\sqrt{3}}l\sin \left( \theta +\frac{\pi}{3} \right)
当夹角 \theta 变化一个小量 \Delta \theta 时，两条边长的变化量为
\Delta a\approx \frac{2}{\sqrt{3}}l\cos \theta \Delta \theta ,\Delta b\approx -\frac{2}{\sqrt{3}}l\cos \left( \theta +\frac{\pi}{3} \right) \Delta \theta
根据 \bigtriangleup DAE \text{∽} \bigtriangleup IEG ，得 IE 长度
\Delta a^*\approx \Delta a\frac{b}{a}\approx \frac{2}{\sqrt{3}}l\cos \theta \frac{\sin \left( \theta +\frac{\pi}{3} \right)}{\sin \theta}\Delta \theta
同样根据相似三角形， \bigtriangleup DFH 和 \bigtriangleup EIH 的高之比为
\frac{h_1}{h_2}=\frac{\Delta b}{\Delta a^*}\approx \frac{-\frac{2}{\sqrt{3}}l\cos \left( \theta +\frac{\pi}{3} \right) \Delta \theta}{\frac{2}{\sqrt{3}}l\cos \theta \frac{\sin \left( \theta +\frac{\pi}{3} \right)}{\sin \theta}\Delta \theta}=-\frac{\tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right)}
所以
h_1=\frac{\sqrt{3}}{2}a\frac{-\frac{\tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right)}}{1-\frac{\tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right)}}=\frac{\sqrt{3}}{2}a\frac{-\tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right) -\tan \theta}
\Delta S_1=\frac{1}{2}\Delta bh_1 \\=\frac{1}{2}\frac{2}{\sqrt{3}}l\cos \left( \theta +\frac{\pi}{3} \right) \Delta \theta \frac{\sqrt{3}}{2}\frac{2}{\sqrt{3}}l\sin \theta \frac{-\tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right) -\tan \theta} \\ =\frac{1}{\sqrt{3}}l^2\frac{-\sin \theta \cos \left( \theta +\frac{\pi}{3} \right) \tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right) -\tan \theta}\Delta \theta
S_1=\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}{\frac{1}{\sqrt{3}}l^2\frac{\sin \theta \cos \left( \theta +\frac{\pi}{3} \right) \tan \theta}{\tan \left( \theta +\frac{\pi}{3} \right) -\tan \theta}d\theta} \\=\frac{l^2}{\sqrt{3}}\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}{\frac{\sin ^2\theta \cos ^2\left( \theta +\frac{\pi}{3} \right)}{\sin \left( \theta +\frac{\pi}{3} \right) \cos \theta -\sin \theta \cos \left( \theta +\frac{\pi}{3} \right)}d\theta} \\ =\frac{5l^2}{288}\left( 2\pi -3\sqrt{3} \right)
扫过的总面积为 \frac{5l^2}{144}\left( 2\pi -3\sqrt{3} \right) +\frac{\sqrt{3}}{4}l^2=\left( \frac{7}{48}\sqrt{3}+\frac{5}{72}\pi \right) l^2
3 Likes
有点像逻辑斯蒂增长模型，生物种群 S 型增长
2 Likes
这是上帝的旨意。
1 Like
似乎 KaTeX 没有 \boldsymbol，只有 \vec 吧？比如 \vec{a} 等．
现在这样有点像黑箱，得猜公式里面有啥
1 Like
刷新一下试试？
正常现实啦