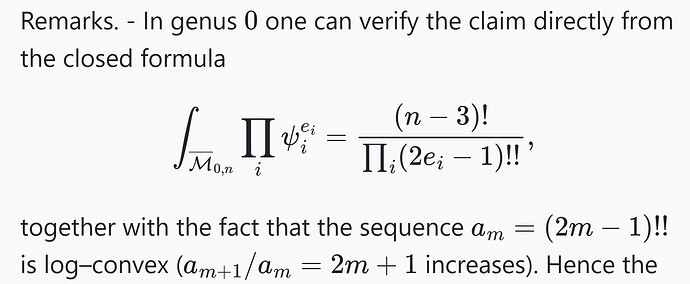Zethes
December 18, 2025, 6:16pm
1
作者:马丁·克勒普曼(Martin Kleppmann)
发布日期:2025 年 12 月 8 日
人们已经广泛讨论过人工智能(AI)对软件开发的影响,但有一个角度我还没怎么见到有人提及:我相信,AI 将使形式化验证(formal verification)——这一数十年来一直被视为小众甚至边缘领域的技术——真正进入软件工程的主流。
像 Rocq、Isabelle、Lean、F* 和 Agda 这样的证明助手(proof assistants)和以证明为导向的编程语言已存在多年。它们允许开发者为一段代码编写形式化的规范(specification),然后通过数学方式证明该代码在所有情况下(包括你未曾想到的奇怪边界情况)都满足该规范。这些工具已被用于开发一些大型的形式化验证软件系统,例如操作系统内核、C 语言编译器和加密协议栈。
目前,形式化验证主要局限于研究项目,工业界的软件工程师(即使是在医疗设备和航空等传统高可靠性领域工作的工程师)很少使用形式化方法。原因在于编写这些证明既极其困难(通常需要博士级别的训练),又极其耗时。
例如,截至 2009 年,经过形式化验证的 seL4 微内核包含 8,700 行 C 代码,但完成其正确性证明却耗费了 20 人年的工作量,以及 20 万行 Isabelle 证明代码——这意味着每行实现代码平均需要 23 行证明代码和半天的人力。此外,据我粗略估计,全世界大概只有几百人真正懂得如何编写这类证明,因为这需要大量关于证明系统本身的深奥知识。
用简单的经济学术语来说:对大多数系统而言,由 bug 带来的预期成本,低于使用形式化验证技术以彻底消除这些 bug 的预期成本。部分原因或许是 bug 本质上是一种“负外部性”:承担 bug 成本的往往不是开发者,而是最终用户。但即使开发者自己承担全部成本,形式化验证依然过于困难和昂贵。
至少,这在最近之前确实是事实。如今,基于大语言模型(LLM)的编程助手不仅在编写实现代码方面表现越来越出色,甚至还能编写多种语言的证明脚本。目前,这一过程仍需具备专业知识的人类加以引导,但我们不难推断:在接下来的几年内,这一过程有望实现完全自动化。一旦如此,形式化验证的经济性将发生根本性转变。
如果形式化验证变得极其便宜,我们就能验证更多软件。不仅如此,AI 本身也催生了对形式化验证的更大需求:与其让人去审查 AI 生成的代码,我更愿意让 AI 向我证明它生成的代码是正确的。如果它能做到这一点,我宁愿选择 AI 生成的代码,而不是充满“手工匠气 bug”的人工代码!
事实上,我认为编写证明脚本正是 LLM 最理想的应用场景之一。因为即使 LLM 产生了胡言乱语(hallucination),证明检查器(proof checker)也会拒绝任何无效的证明,并强制 AI 重新尝试 。而证明检查器本身通常是一小段经过验证的代码,几乎不可能让无效证明蒙混过关。
当然,这并不意味着软件会突然变得毫无 bug。随着验证过程本身日益自动化,挑战将转移到正确地定义规范上:也就是说,你如何确定所证明的性质,正是你真正关心的性质?阅读和编写这类形式化规范仍然需要专业知识和深思熟虑。但与手写证明相比,编写规范要容易且快速得多——这本身就是巨大进步。
我甚至可以想象,未来的 AI 代理还能协助编写规范,实现形式语言与自然语言之间的相互翻译。虽然翻译过程中可能会丢失一些细微差别,但这种风险似乎是可控的。
想到未来我们只需以高级、声明式的方式指定一段代码应有的性质,AI 就能“凭直觉”(vibe code)生成实现代码以及证明其满足规范的证明,这令我感到无比兴奋。这将彻底改变软件开发的本质:我们甚至不再需要查看 AI 生成的代码,就像我们从不查看编译器生成的机器码一样。
总结一下:
形式化验证即将变得极其廉价;
AI 生成的代码需要形式化验证,这样我们才能跳过人工审查,仍可确信其正确性;
形式化验证的精确性正好弥补了 LLM 的模糊性和概率性。
这三点共同作用,意味着形式化验证很可能在可预见的未来走向主流。我猜测,届时限制其普及的将不再是技术本身,而是人们观念上的转变——即意识到形式化方法如今已在实践中变得切实可行。
2 Likes
Zethes
December 18, 2025, 6:23pm
2
AI+ 形式化证明 正在改变数学界的工作方式
陶哲轩(Terence Tao) 有多个文章、博客帖子和演讲表达了与 Martin Kleppmann 高度相似的观点:AI 将大幅降低形式验证(formal verification)和证明助手(如 Lean)的成本,推动其在数学和软件工程中变得主流,甚至成为标准实践 。
关键文章与演讲 :
2024 年 AMS Colloquium Lecture“Machine Assisted Proofs” (YouTube,基于 Notices of the American Mathematical Society 文章):系统讨论机器辅助证明历史与未来,强调 AI + 证明助手(如 Lean)可实现大规模协作、自动化验证,甚至生成完整论文 + 形式证明。预测形式化将成为常态,AI 作为“数学家的副驾驶”。博客系列(terrytao.wordpress.com ) :
“Formalizing the proof of PFR in Lean4 using Blueprint”(2023):描述用 AI 辅助在 Lean 中形式化复杂证明,强调 AI 填补小缺口潜力。
“A slightly longer Lean 4 proof tour”(2023):认为 AI 近期目标是自动关闭证明中的“小 sorry”(未证明部分),加速蓝图到形式证明转换。
“A tool to verify estimates, II: a flexible proof assistant”(2025):开发仿 Lean 的轻量证明助手,计划集成 AI 生成伪证明后转正式 Lean 验证。
“Machine assisted proofs”PDF 与相关帖子:讨论 AI 与证明助手结合,验证 LLM 输出,推动形式方法普及。
采访(如 Scientific American, 2024) :AI 将成为数学家“副驾驶”,未来解释证明给 GPT,它生成 Lean 代码并验证。形式化成本将低于传统写作,推动广泛采用。其他实践 :陶哲轩亲自用 GitHub Copilot + AI 在 Lean 中形式化证明(如 PFR 猜想、Analysis I 教材),并发现手动证明中隐藏错误,证明形式验证 + AI 的实用价值。
陶哲轩虽主要聚焦数学证明形式化,但其观点直接适用于软件工程:AI 生成代码 + 证明可跳过人工审查,确保正确性,与 Kleppmann“AI 生成代码需形式验证以信任”高度一致。他乐观预测这将很快成为数学(及相关领域)主流。
Zethes
December 18, 2025, 6:26pm
3
证明助手(也叫交互式定理证明器)是一种帮助人类用计算机严格证明 数学定理或验证软件/硬件正确性的工具。
形式化证明 :把数学命题和证明过程完全用精确的逻辑语言写出来,计算机能 100% 检查。证明检查器 :工具的核心部分很小(小内核原则),本身被严格验证,几乎不可能出错。即使人或 AI 写出错误证明,它也会拒绝。柯里 - 霍华德同构 :证明 ↔ 程序。写一个证明的过程就像写一个满足规格的程序(这也是很多证明助手同时支持代码生成的原因)。
1967 年:Automath,第一个形式化数学系统。
1980 年代:Coq、Isabelle 诞生,四色定理首次被机器验证。
1994 年:英特尔奔腾芯片浮点 bug 损失 4.75 亿美元,推动工业界重视形式验证。
2009 年:seL4 操作系统内核被完全形式化验证(世界上第一个)。
2010 年代:Lean 出现,Mathlib 数学库快速增长。
2023–2025 年:AI 大爆发——DeepMind 的 AlphaProof、DeepSeek-Prover、OpenAI 等用 AI+ 证明助手解决 IMO(国际数学奥林匹克)难题,标志 AI 开始大幅降低证明成本。
软件/硬件验证
操作系统内核(如 seL4)
编译器(如 CompCert,保证编译后代码不引入 bug)
密码协议、区块链智能合约、航空/医疗设备软件
避免灾难性 bug(比如芯片设计错误、分布式系统一致性问题)
数学大定理证明
四色定理、开普勒猜想、费马大定理、奇数阶有限单群分类等
建立大规模机器验证数学库(Lean 的 Mathlib、Isabelle 的 AFP)
编程语言设计
工具
特点亮点
代表项目/成就
Lean 4 速度快、自动化强、社区活跃、AI 友好
Mathlib 最大数学库;IMO 银牌(AlphaProof)
Rocq/Coq 历史最久、代码生成强、小内核可靠
CompCert 编译器、seL4 早期验证
Isabelle 高阶逻辑、文档生成好、工业应用多
seL4 完整验证、Archive of Formal Proofs
F *专为程序验证 + 代码生成设计
安全关键软件、加密协议
Agda 依赖类型纯度高,适合理论研究
HOL Light/HOL4 极简内核、数学证明强
开普勒猜想证明
AI 与证明助手的结合 :大型语言模型(LLM)能自动生成证明草稿,证明检查器负责把关,彻底改变“写证明太贵太难”的局面。代表成果:谷歌 DeepMind、OpenAI、DeepSeek 等已在 Lean 上实现高难度数学题自动证明。
未来预期:形式化证明成本大幅下降,可能像编译器一样成为软件开发的标配;数学家只需提供高层次思路,AI 填细节并验证。
Zethes
December 18, 2025, 6:31pm
4
这个 GitHub 仓库 是陶哲轩于2025 年 5 月 31 日 正式启动的一个开源项目,目的是将他的经典实分析教材《Analysis I》(本科生水平)用Lean 4 证明助手进行形式化翻译。
忠实复述原书 :尽可能贴近教材的定义、定理和证明结构,同时展示 Lean 的语法和特性(不追求最高效率,有时会偏离 Lean 的“习惯用法”)。作为伴侣资源 :不是取代原书,而是提供一个“带注释的伴侣”。书中留给读者的习题在这里用 sorry(占位符)表示,鼓励读者自己 fork 仓库填写证明。不直接引用原书文字 :只给出原书章节引用,避免版权问题。与 Mathlib 兼容 :早期章节独立定义(如第 2 章自己构建自然数),后期逐步切换到 Lean 标准数学库Mathlib 的定义(并在章节结尾证明两者同构),这样既教学又实用。
序列从0 开始索引 (原书从 1 开始),因为 Mathlib 对ℕ(从 0 开始)的支持更好。
一些原书未定义的操作(如除以 0、非 Cauchy 序列的极限)被赋“垃圾值”(如 0),确保函数是全定义的 (total function)。Lean 对全函数支持更好,避免部分函数带来的证明复杂性(“dependent type hell”)。
第 2 章自然数用归纳类型构造(而非纯公理化),但在结尾证明了 Peano 公理。
项目进展非常快,已基本覆盖全书主要内容(第 1 章引言未形式化):
第 2 章 :自然数(Peano 公理、加法、乘法)+ 与 Mathlib 同构。第 3 章 :集合论基础、函数、像与原像、笛卡尔积、基数等。第 4 章 :整数、有理数、绝对值、指数、理性数的间隙。第 5 章 :实数构造(Cauchy 序列)、序、最小上界界、实指数等 + 与 Mathlib 实数同构。第 6 章 :序列极限、扩展实数、上下极限、标准极限、子序列等。第 7 章 :级数(有限、无限、非负和、重排、根检验/比检验)。第 8 章 :无穷集合(可数、不可数、选择公理、有序集)。第 9 章 :ℝ上连续函数(子集、极限、连续性、中值定理、一致连续等)。第 10 章 :导数(基本定义、单调性、反函数导数、L’Hôpital 法则)。第 11 章 :Riemann 积分(分划、上/下积分、可积性、基本定理等)。附录 A :数学逻辑基础(语句、蕴涵、量词、相等等)。附录 B :十进制表示。
此外,还有一些额外内容:
陶哲轩的《测度论》书籍形式化(进行中)。
物理单位系统形式化(包括 SI 单位)。
有限选择公理(避免使用 Lean 的选择公理)。
有限概率论及几个 Erdős 问题的解。
社区活跃 :1.4k 星、181 fork、36 位贡献者,最近提交在几天前。文档网站 :Partial Lean formalization of Analysis I — Verso (每个章节有 Verso 页面、文档和 Lean 源代码)。资源 :仓库提供构建脚本、Lean 社区链接、Mathlib 搜索工具等。陶哲轩的 YouTube 频道有相关演示。这体现了陶哲轩对 AI+ 证明助手的乐观态度:项目中使用 GitHub Copilot 等工具加速形式化,正如他之前预测的,AI 正让形式验证变得更易普及。
这个项目不仅是《Analysis I》的“机器可验证版本”,还是学习 Lean 和 Mathlib 的绝佳入门材料,尤其适合想结合教材和形式化证明的学生/研究者。如果你感兴趣,可以直接 clone 仓库尝试填写 sorry 部分!
Zethes
December 18, 2025, 6:52pm
5
Bartosz Naskręcki @UAM_Poznan | Researcher @ccaiwut | Rigorous mathematics, programming &ML | Passionate about what AI really understands
例子:这位数学家通过 HarmonicMath 加速完成数学定理的形式化证明。
数学论文需要形式化验证。通常,这一过程由审稿人非正式地完成。但如果我们能依赖更可靠的方式,例如自动形式化为 Lean 4 代码,从而将审稿人的角色简化为对定义和定理表述进行细致检查,那会怎样?此时,自动生成代码的编译结果本身就会成为一份证明证书。这正是我与 @HarmonicMath 的 Aristotle 在一次长期运行中所实现的成果。
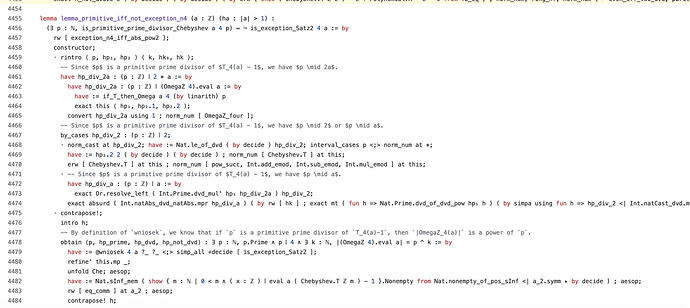
感谢 @PietroMonticone 和 @llllvvuu 在蓝图(blueprint)搭建过程中的帮助。在此,我展示了一篇我朋友 Stefan Barańczuk 关于切比雪夫整除序列(Chebyshev divisibility sequences)论文的完整、正确的自动形式化成果。该代码包含约 5000 行高度非平凡的 Lean 代码,不仅修正了原论文中的各种不一致之处和漏洞,甚至证明了一些原本被省略的命题。
相关成果可见:
我将陆续发布一系列此类实验,以证明在某些数学领域——包括初等数论、组合数学和分析(即 Mathlib 所涵盖的各类内容)——我们距离大规模转变数学证明有效性的文档方式已经不远了。我认为,这一年将会非常忙碌!
如果我是今天的一名学生,与最前沿的大语言模型互动几乎会让我觉得是在“作弊”。今天早上,我随手拍了一张黑板的照片,让 ChatGPT-5.2-Pro 解释其中的背景、解法,以及关于切瓦雷(Chevalley)关于可构造集(constructible sets)著名定理的一些补充评论。我收到的竟是一份极为深入的报告,它综合了来自全网的高质量代数几何材料,内容之精炼与深刻令人惊叹。
这引发了一个严肃的问题:当今学生真正面对的努力与挑战究竟是什么?成本固然是一个因素,但一旦能够使用这些模型,我们该如何在这个信息丰裕的时代学习?在这个时代,解释、参考文献和交互式探索几乎都能即时获取。
也许,真正的困难已不再是如何获得信息,甚至也不再是如何理解某个孤立的论证,而在于培养判断力:懂得提出什么样的问题,知道哪些解释值得信任,能够分辨深刻洞见与表面合理的区别,并将思想真正内化,而非仅仅消费内容。在一个答案唾手可得的环境中,真正的挑战或许在于如何形成品味、数学直觉,以及在知识突然泛滥的洪流中学会航行——而非沉没其中。
Zethes
December 18, 2025, 6:56pm
6
@HarmonicMath Building Mathematical Superintelligence
Harmonic 由 Robinhood 创始人兼 CEO Vlad Tenev 与 Tudor Achim 共同创立,致力于开发一种新型的人工智能系统——Mathematical Superintelligence (MSI,数学超智能),其目标是让 AI 具备接近甚至超越人类顶尖数学家的形式化推理与证明能力 。
该实验室的代表性成果是名为 Aristotle 的 AI 系统。Aristotle 在 2025 年国际数学奥林匹克竞赛(IMO)中取得了历史性金牌水平的表现 ,并在标准数学推理评测(如 MiniF2F)上达到了 90% 的准确率 。更引人注目的是,Aristotle 曾在6 小时内解决了一个困扰数学界 30 年的公开问题 ,展示了其强大的问题求解能力。
Harmonic 强调,真正的智能不应只关注答案,而应关注推理过程的正确性 :“当我们想知道一个答案是否正确时,我们检查的是推理——那些逻辑步骤”。其长远愿景是让数学超智能不仅成为研究工具,还能被广泛、公平地使用 :“数学超智能即将到来,它应当被均匀分布”。
截至 2025 年底,Harmonic 已获得1 亿美元融资 并晋升为“独角兽”企业,显示出业界对其技术路线的高度认可。
Harmonic 的 x 账号被人工智能和数学领域的知名学者关注。
Chieh-Hsin (Jesse) Lai (@JC JesseLai)
身份 :目前是索尼 AI(Sony AI)的研究员,同时也是纽约城市大学(NYCU)应用数学系的访问助理教授。背景 :拥有明尼苏达大学(U. of Minnesota)的数学博士学位。领域 :他的研究横跨数学与人工智能,是扩散模型领域和流模型领域的领军人物,尤其关注扩散模型在音乐合成中的应用。他个人网站 chiehhshinjesselai.github.io 可能展示其更详细的研究成果。
Christian Szegedy (@ChrSzegedy )
身份 :人工智能领域的研究科学家。领域 :他是深度学习领域的先驱之一,以其在计算机视觉和神经网络架构方面的工作而闻名。他参与了 Google Brain 团队,并对 Inception 架构等有重要贡献。观点 :他明确表示“Opinions are mine.”(观点仅代表个人),表明他在社交媒体上分享的是个人见解。
Emily Riehl (@emilyriehl )
身份 :范畴论专家、在职数学家。领域 :她是现代范畴论领域的领军人物,尤其在高阶范畴论和同伦理论方面有深入研究。她致力于将抽象的范畴论概念应用于更广泛的数学领域,并以清晰的教学风格著称,著有《Category Theory in Context》等教材。
François Chollet (@fchollet )
身份 :Keras 框架的创建者,ARC-AGI 和@ndea 的联合创始人,《Python 深度学习》一书的作者。领域 :他是人工智能界最具影响力的人物之一。他开发的 Keras 库极大地简化了深度学习模型的构建过程,推动了该领域的普及。他目前专注于通用人工智能(AGI)的研究,特别是通过 ARC-AGI 竞赛来探索和评估机器的抽象推理能力。
Zethes
December 18, 2025, 7:31pm
8
ETH Zurich 的数学家 Johannes Schmitt 宣布了一个重要的里程碑:OpenAI 的 GPT-5 模型首次完全自主 地解决了一个数学领域的开放问题(open math problem),提供了完整且正确的证明,没有任何人类提示或干预。
具体内容是关于枚举几何(enumerative geometry)中的一个小但新颖的贡献:涉及曲线模空间(moduli spaces of curves)上的交数(intersection numbers)。作者咨询了领域专家,确认这个问题此前是未解决的,没有明显的解法,于是提交到他参与的基准项目 IMProofBench(一个测试 AI 数学证明能力的平台)。
GPT-5 给出了一个优雅的证明,竟然绕过了该领域传统的复杂理论,而是从代数几何的另一个分支借用技术,提供了“局外人视角”的新思路。
随后,他们合作撰写了一篇论文,整合了多个 AI 模型的贡献(如 GPT-5 和 Gemini 3 Pro 的证明、Claude 的写作辅助、Lean 形式化验证 ),并透明标注了每段内容的 AI/人类来源,还附上提示日志。这被视为人-AI 协作的新实验。
有趣的结尾:GPT-5 在给出完美一般证明后,在一个特殊案例的示例公式上出现了幻觉(hallucination,完全编造错误内容),后来被另一个 AI(Claude)指出。
幻觉示例
总体来说,这个帖子标志着 AI 在高级数学研究中从“辅助工具”向“独立发现者”迈出关键一步,引发了数学和 AI 社区的广泛讨论。
For the pure $ψ$-class intersection numbers $D(\textbf{e})=\langle τ_{e_1} \cdots τ_{e_n} \rangle_g$ on the moduli space $\overline{\mathcal{M}}_{g,n}$ of stable curves, we determine for which choices of $\textbf{e}=(e_1, \ldots, e_n)$ the value of...
Zethes
December 18, 2025, 7:40pm
9
https://leanprover.zulipchat.com/#narrow/channel/219941-Machine-Learning-for-Theorem-Proving/topic/AI-discovered.20proof.20on.20psi-integrals.20.28with.20Lean.20formalizat.2E.29/near/563828163
背景与数学结果
问题来源 :Schmitt 参与了一个叫IMProofBench 的项目。这是一个专为测试 AI 在研究级数学证明 能力的基准测试项目(private benchmark,避免数据污染)。项目收集了多名数学家提交的 PhD 水平开放问题。
具体问题 :在稳定曲线模空间 \overline{\mathcal{M}}_{g,n} 上,纯ψ类交数(descendant integrals):
D(\mathbf{e}) = \langle \tau_{e_1} \cdots \tau_{e_n} \rangle_g = \int_{\overline{\mathcal{M}}_{g,n}} \psi_1^{e_1} \cdots \psi_n^{e_n}
其中 \sum e_i = 3g-3+n
问题 :对于固定 g,n,哪些指数向量 \mathbf{e} = (e_1, \dots, e_n) 使这个交数最大 ?
结果 :最大值在balanced 向量 上取得,即 e_i 们尽可能均匀分布(相邻差至多 1)。最小值在集中向量(几乎所有质量在一个位置)上取得。
证明思路 :AI(GPT-5)给出了一个简洁证明,完全绕过传统理论(如 Witten-Kontsevich 定理),只用ψ类的抽象交数性质:nefness (nef 类)和Khovanskii-Teissier 不等式 (log-concavity)。
论文 :Schmitt 迅速写成论文上传 arXiv(arXiv:2512.14575,标题《Extremal descendant integrals on moduli spaces of curves: An inequality discovered and proved in collaboration with AI》)。论文中明确标注 AI 贡献的部分(包括整段文字由 AI 撰写),并附提示日志以示透明。
这是一个里程碑:这是已知第一个 AI 独立解决研究级开放数学问题 的公开案例(此前 AI 多在竞赛题或已知问题上表现)。
AI 的具体贡献
GPT-5 首先生成自然语言证明(被 Schmitt 和同事验证正确)。
其他 AI(如 Gemini 3 Pro、Claude Opus 4.5)帮助起草论文大段文字。
GPT-5.2 和 Claude Code 帮助生成 Lean 代码。
Schmitt 本人无 Lean 经验 ,一天内用 AI“vibe-coding”(随意生成 + 迭代)完成形式化。
Lean 形式化部分 形式化好处:优化部分充满繁琐不等式,容易出错;Lean 验证后让人放心 。Schmitt 认为这占了“50% 验证收益”,但只需“0.01% 工作量”(相比形式化整个代数几何背景)。
社区讨论的焦点
惊喜与赞赏 :很多人惊叹 AI 解决开放问题、零经验下形式化 Lean(“vibe-formalizing”)。
Kevin Buzzard (Lean 社区大牛)指出:模空间定义本身是巨大空白(甚至椭圆曲线模空间对 Fermat 最后定理都缺),形式化几何部分可能需多年。强调 AI 不可信赖定义,但可辅助填补小 lemma。
形式化 AI 证明的规范 :讨论如何处理 AI 生成代码的信任问题。
建议:定义放单独文件 + 大警告,必须人工审查。
避免 mathlib 碎片化:优先推入主库。
讨论“quarantine”无证明义务的定义,便于审查。
更广哲学讨论 (Timothy Chow 等):
mathlib 是否应成“唯一正典”定义源?但数学概念往往有多个等价定义(A 类),或不等价但相关约定(B 类,如 Fourier 变换归一化)。
形式化是否完全捕捉数学的“非形式含义”?(如“可证明性”概念的细微差别、Gödel 不完备性、数学家的“直觉”)。
Kevin Buzzard:实际论文中的定理(如 Sylow)不依赖底层基础接线。
意义与启示
AI 在数学研究中的角色 :这例显示前沿 AI 已能发现新证明、绕过传统路径、辅助形式化。
未来趋势 :可能出现“人+AI 混合证明”规范、专用模板处理 AI 贡献、mathlib 逐步覆盖更多代数几何。
当前状态 (2025 年 12 月):GPT-5 在 IMProofBench 上表现最佳(完全正确解决 22% 问题),显示 AI 已在辅助研究级数学。
hoist
December 19, 2025, 12:56am
10
充满期待,数学需要形式化验证来整治。但听说现在还比较难用。
1 Like
Zethes
December 19, 2025, 10:05am
11
2025 年 12 月 8 日 —— 著名数学家、菲尔兹奖得奖者陶哲轩(Terence Tao)近日在其个人博客上详述了 Erdős 问题#1026 的完整解决过程。这一源于 1975 年的经典开放问题,通过在线社区协作、人工智能工具以及既有文献的结合,最终在 2025 年 12 月得以彻底解决。
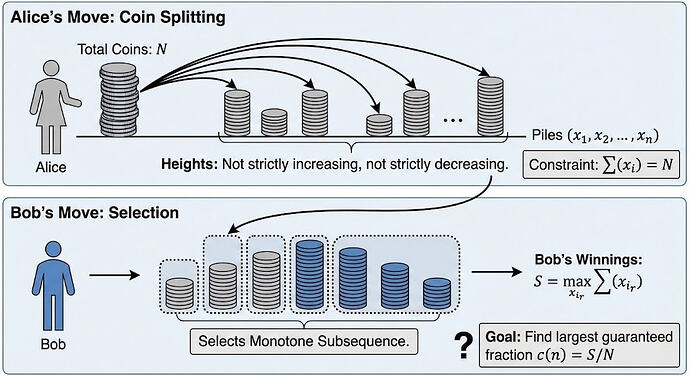
Erdős 问题#1026 源于保罗·埃尔德什(Paul Erdős)对单调子序列的探究。该问题最初表述较为模糊:给定一个 distinct 实数序列 a_1 < a_2 < \dots < a_n ,求最大单调子序列的和的上界。经过社区澄清和重新表述,该问题等价于确定常数 c_k 的精确渐近行为,其中 c_k 表示在总和归一化为 1 的序列中,Bob(选取单调子序列)所能保证的最大份额,而 Alice 试图最小化这一份额。最终证明表明,c_k = 2 / \sqrt{k} 为上界,且在完美平方 k 时精确达成。
解决过程始于 2025 年 9 月 12 日,该问题被正式录入 Erdős 问题网站。社区成员迅速提出博弈论解读,并计算小 k 值,猜测 c_k \sim 2 / \sqrt{k} 。问题一度沉寂近两个月,直至 12 月 7 日,数学家 Boris Alexeev 使用 AI 工具Aristotle (由 Harmonic 公司开发)对该问题进行系统扫描。
Aristotle 在完全自主模式下,仅基于形式化陈述,成功将问题转化为矩形打包问题,并在形式化证明系统Lean 中生成完整证明。这一成就标志着 AI 首次独立产生非平凡数学证明,并直接输出可验证的形式化代码。尽管后续人类审查发现该证明并非全新(源于 1959 年 Seidenberg 的工作变体),但 Aristotle 的自主性和效率令人瞩目——它将一个潜在的猜想直接提升为形式化定理。
紧随其后,社区成员 Koishi Chan 提供基于 Erdős-Szekeres 定理的“blow-up”论证下界,而陶哲轩本人则运用另一 AI 工具AlphaEvolve 生成上界数值证据,并推导出精确构造。最终,Lawrence Wu 通过 AI 深度文献搜索,定位 2024 年 Baek、Koizumi 和 Ueoro 的论文,该文解决了相关的 Erdős 平方打包问题(#106 的轴平行版本),从而严格证明上界 \max \sum_{i \in S} a_i \leq 2 / \sqrt{k} 。这一链接将问题彻底闭合。
陶哲轩在博客中强调:“这一解决过程融合了现有文献、在线协作与多种 AI 工具。”他指出,Aristotle 的 Lean 形式化证明、AlphaEvolve 的优化构造,以及 AI 辅助的文献检索,显著加速了进展。
这一事件是 2025 年 AI 辅助数学突破的最新例证。此前,Aristotle 已独立解决多个 Erdős 问题,并在 Lean 中形式化验证。专家认为,此类工具正重塑数学研究范式:AI 擅长处理文献“暗森林”、生成形式化代码和探索数值模式,从而让人类数学家专注于核心创造性工作。
Erdős 问题网站维护者 Thomas Bloom 表示,该问题现已标记为“已解决”。这一协作模式或将成为未来攻克顽固开放问题的标准路径,预示着人工智能与形式化证明时代在数学领域的全面到来。