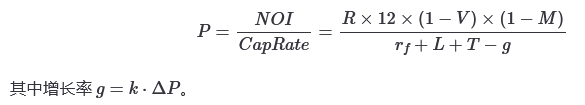由于公式渲染问题,贴张渲染好的图
摘要
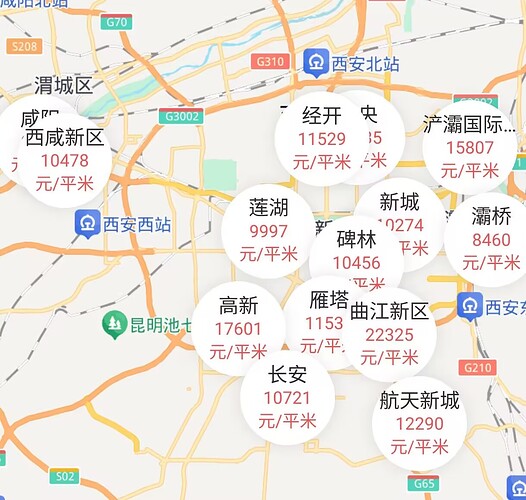
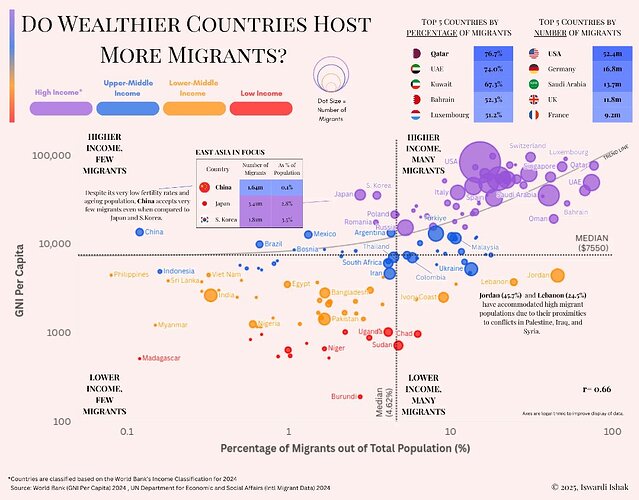
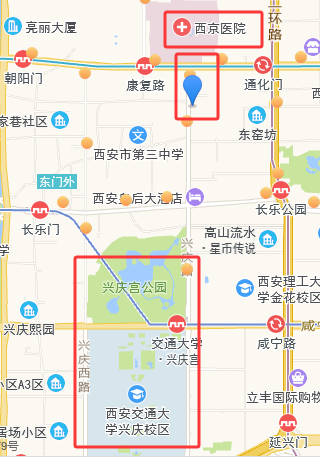
本报告旨在通过房价定价模型,对特定城市的住宅理论价格进行估值。
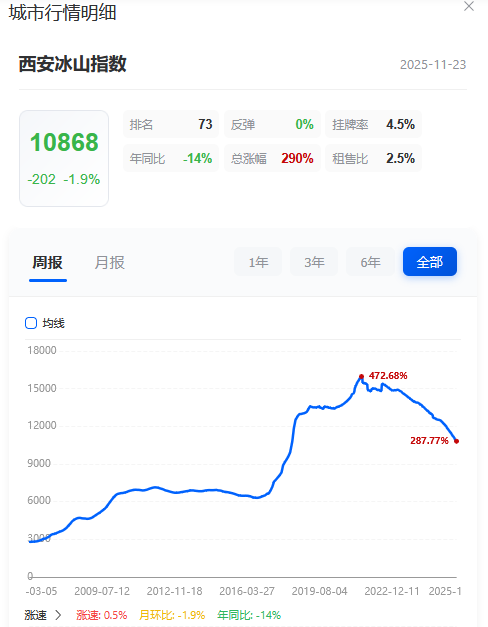
模型引入杰弗里·韦斯特(Geoffrey West)与路易斯·贝当古(Luis Bettencourt)的城市标度律(Urban Scaling Laws),设定人口对租金的弹性系数 k=1.25。以 2024 年西安市人口数据及市场参数为基础,测算出在当前国债收益率与流动性环境下,单位平米的理性估值区间。
模型
城市标度律
根据 Bettencourt 等人的研究《Growth, innovation, scaling, and the pace of life in cities》,城市并非简单的线性放大,而是具有生物有机体般的标度特征。
- 超线性标度 (\beta > 1):社会经济产出(GDP、工资、创新专利、犯罪率等)与人口规模呈 Y \propto N^\beta 关系,其中 \beta \approx 1.15 \sim 1.30。
- 本报告设定:取 k=1.25。这意味着人口每增长 1%,由于集聚效应带来的生产率提升,将推动内生性租金(及预期收入)增长 1.25%。
理性人定价模型
采用戈登增长模型(Gordon Growth Model)的变体,将房产视为一种产生永续现金流的资产。
其中增长率 g = k \cdot \Delta P。
参数测算与分析
- 基础月租金 (R): 30 元/平米。
- 空置率 (V): 10% ------ 反映了摩擦性空置及市场供需错配风险。
- 运营成本率 (M): 15% ------ 涵盖物业费、取暖费、中介佣金、保险及房屋维修基金摊销。
- 无风险利率 (r_f): 2.15% ------ 锚定 30 年期超长期特别国债收益率,代表资金的时间价值。
- 房产税 (T): 0% ------ 暂不考虑持有环节税收。
流动性折价 (L)
由于房产变现周期长(去化周期),且存在价格波动风险,理性投资者要求流动性折价。
当前二线城市二手房平均去化周期较长,假设为 18 个月。相对于 T+0 的股票或债券,房产具有极高的非流动性成本。参考私募地产基金(PERE)标准,流动性溢价通常在 1.5\% \sim 3.0\% 之间。
设定:取 L = 2.25\%。
增长率($g$)
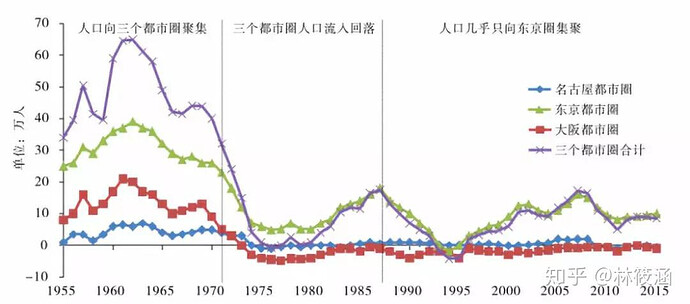
人口流入率 (\Delta P)
根据西安统计数据:
- 2024 年末常住人口:1316.76 万人
- 当年增量:8.94 万人
- 人口增长率 (\Delta P):
$$ \Delta P = \frac{8.94}{1316.76 - 8.94} \approx 0.6836% $$
基于城市标度律弹性系数 k=1.25:
$$ g = k \times \Delta P = 1.25 \times 0.6836% \approx 0.8545% $$
注:此为名义增长率,假设通胀环境温和。
计算代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
class RealEstateValuation:
def __init__(self, R, V, M, rf, T, pop_current, pop_increase, k=1.25):
"""
初始化估值模型参数
:param R: 月租金 (元/平米)
:param V: 空置率 (0-1)
:param M: 维护费用比例 (0-1)
:param rf: 无风险利率 (0-1)
:param T: 房产税率 (0-1)
:param pop_current: 当前年末人口
:param pop_increase: 当年新增人口
:param k: 城市标度律弹性系数 (默认为 1.25)
"""
self.R = R
self.V = V
self.M = M
self.rf = rf
self.T = T
self.k = k
# 计算人口增长率 delta_P
pop_start = pop_current - pop_increase
self.delta_P = pop_increase / pop_start
# 计算年净营运收入 (NOI)
self.noi = self.R * 12 * (1 - self.V) * (1 - self.M)
def calculate_price(self, L):
"""
计算理性房价
:param L: 流动性折价/风险溢价 (0-1)
:return: 估值 (元/平米), 资本化率
"""
# 增长率 g = k * delta_P
g = self.k * self.delta_P
# 分母:r_f + L + T - g
cap_rate = self.rf + L + self.T - g
# 安全检查:防止分母为负或过小 (意味着增长率超过了折现率,导致价格无穷大)
if cap_rate <= 0.001:
return np.inf, cap_rate
price = self.noi / cap_rate
return price, cap_rate
def sensitivity_analysis(self):
"""
敏感性分析:流动性折价 (L) vs 人口流入率变化 (Delta P)
"""
# 设定 L 的变化范围:1.5% 到 3.0%
l_range = np.linspace(0.015, 0.03, 15)
# 设定人口流入率的变化范围
# 当前增速约为 0.68%,我们模拟 -0.5% 到 2.0%
p_growth_range = np.linspace(-0.005, 0.02, 25)
results = np.zeros((len(l_range), len(p_growth_range)))
print(f"{'='*60}")
print("基准数据分析 (Base Case):")
print(f"NOI (年净收入): {self.noi:.2f} 元/平米")
print(f"实际人口增长率:{self.delta_P*100:.4f}%")
print(f"租金预期增长率 (g): {self.k * self.delta_P * 100:.4f}%")
print(f"{'='*60}\n")
# 存储用于绘图的数据
df_heatmap = pd.DataFrame(index=[f"L={x*100:.1f}%" for x in l_range],
columns=[f"ΔP={x*100:.2f}%" for x in p_growth_range])
for i, l_val in enumerate(l_range):
for j, p_val in enumerate(p_growth_range):
# 临时覆盖 delta_P 进行模拟
original_delta_p = self.delta_P
self.delta_P = p_val
price, _ = self.calculate_price(l_val)
results[i, j] = price
df_heatmap.iloc[i, j] = int(price)
# 恢复 delta_P
self.delta_P = original_delta_p
return df_heatmap
# ============================
# 执行计算
# ============================
# 输入参数
xi_an_params = {
'R': 30, # 月租金 30 元/平米
'V': 0.10, # 空置率 10%
'M': 0.15, # 维护费 15%
'rf': 0.0215, # 30Y 国债 2.15%
'T': 0.00, # 税 0%
'pop_current': 1316.76, # 年末人口
'pop_increase': 8.94 # 新增人口
}
# 实例化模型
model = RealEstateValuation(**xi_an_params)
# 1. 计算不同流动性折价下的基准估值
liquidity_scenarios = [0.015, 0.0225, 0.030] # 乐观 (1.5%), 中性 (2.25%), 悲观 (3.0%)
print(f"{'流动性折价 (L)':<15} | {'估值 (元/平米)':<15}")
print("-" * 40)
for liq in liquidity_scenarios:
price, cap_rate = model.calculate_price(liq)
print(f"{liq*100:.2f}%{' ':<15} | {price:,.2f}")
print("\n")
# 2. 敏感性分析矩阵
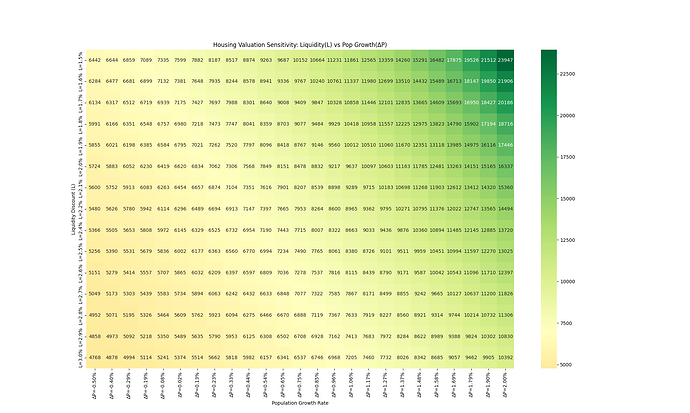
df_results = model.sensitivity_analysis()
print("敏感性分析矩阵 (房价估值:元/平米):")
print("行:流动性折价 (L), 列:人口增长率 (ΔP)")
print(df_results)
try:
plt.figure(figsize=(20, 12))
sns.heatmap(df_results.astype(float), annot=True, fmt=".0f", cmap="RdYlGn", center=7000)
plt.title("Housing Valuation Sensitivity: Liquidity(L) vs Pop Growth(ΔP)")
plt.xlabel("Population Growth Rate")
plt.ylabel("Liquidity Discount (L)")
plt.savefig("heatmap.png")
print("\n[注]:热力图已生成。")
except Exception as e:
print(e)
print("绘图库不可用。")
结果
流动性折价 (L) | 估值 (元/平米)
1.50% | 9,851.46
2.25% | 7,767.54
3.00% | 6,411.32
敏感性分析矩阵 (不同人口净增速 不同流动性折价 的 定价结果)