-
课本:光电效应.pdf (5.0 MB)
-
实验报告要求:
Python scripts (by Gemini 2.5 Flash):
1.py:
import numpy as np
import matplotlib.pyplot as plt
# ======================================================================
# 1. 伏安特性曲线 (I-U 曲线)
# ----------------------------------------------------------------------
# 请替换为你的实验数据
# U_AK: 阳极电压 (V)
# I1_raw: 光电流 I1 (例如,d=4mm) (以 10^-11 A 为单位)
# I2_raw: 光电流 I2 (例如,d=2mm) (以 10^-11 A 为单位)
# 注意:数据应该与你记录的表格 (如 表 3-1-1) 中的电压点对应.
U_AK = np.array(
[
-2.0,
-1.5,
-1.0,
-0.5,
0.0,
0.5,
1.0,
1.5,
2.0,
4.0,
6.0,
8.0,
10.0,
12.0,
14.0,
16.0,
18.0,
20.0,
22.0,
24.0,
26.0,
28.0,
30.0,
]
) # 示例电压值
# 假设的光电流数据 (请务必替换为你测量的实际数据)
I1_raw = np.array(
[
-0.08,
-0.03,
-0.02,
0.59,
2.39,
4.89,
7.27,
9.15,
9.70,
14.1,
18.1,
21.3,
25.2,
27.4,
28.9,
30.9,
31,
31.5,
33.4,
34.6,
35.3,
37.3,
37.8,
]
)
I2_raw = np.array(
[
-0.05,
-0.02,
-0.01,
0.05,
0.24,
0.59,
1.02,
1.73,
2.32,
4.23,
4.79,
5.66,
7.06,
7.69,
8.36,
8.4,
9.1,
9.6,
9.8,
9.9,
10.1,
10.6,
10.9,
]
)
# 将电流单位从 10^-11 A 转换为 10^-10 A 或 10^-12 A (根据你使用的量程和图表要求调整)
# 假设最终绘图单位为 10^-11 A
I1 = I1_raw
I2 = I2_raw
# 绘图
plt.rcParams["font.family"] = "FandolFang"
plt.figure(figsize=(8, 5))
plt.plot(U_AK, I1, "ro-", label=r"$d_1=4mm, \lambda=546nm$ (光强 $E_1$)") # 假设 d1=4mm
plt.plot(
U_AK, I2, "bs--", label=r"$d_2=2mm, \lambda=546nm$ (光强 $E_2$ - 较弱)"
) # 假设 d2=2mm
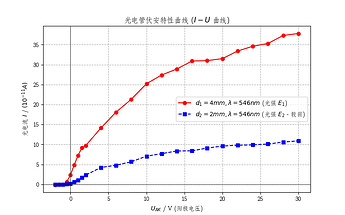
plt.title("光电管伏安特性曲线 ($I-U$ 曲线)")
plt.xlabel(r"$U_{AK}$ / V (阳极电压)")
plt.ylabel(r"光电流 $I$ / $(10^{-11} A)$")
plt.grid(True, linestyle="--")
plt.legend()
plt.axhline(0, color="black", linewidth=0.5) # 绘制 I=0 轴
plt.axvline(0, color="black", linewidth=0.5) # 绘制 U=0 轴
#plt.text(-1.8, I1[-1] * 1.05, r"$I_{H1}$", color="red")
#plt.text(-1.8, I2[-1] * 1.05, r"$I_{H2}$", color="blue")
plt.savefig("1.png")
# 结果分析:I-U 曲线应具有和教材图 3-3 相似的形状,并显示光强越大饱和电流越大 ($I_{H1} > I_{H2}$)
2.py:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# ======================================================================
# 2. 光电特性图线 (饱和光电流 $I_H$ - 光强 $d^2$ 图)
# ----------------------------------------------------------------------
# 请替换为你的实验数据
# d_mm: 光阑孔径 (mm)
# I_H_raw: 饱和光电流 IH (以 10^-11 A 为单位)
d_mm = np.array([2.0, 4.0, 8.0]) # 示例光阑孔径 (mm)
# 假设的光电流数据 (请务必替换为你测量的实际数据,确保 U_s=25V, lambda=577nm)
I_H_raw = np.array([8.9, 35.1, 141.4])
# 数据处理
d_square = d_mm**2 # 计算 d^2 (mm^2)
I_H = I_H_raw # 假设最终绘图单位为 10^-11 A
# 线性拟合模型:I_H = k * d^2 + b
def linear_func(x, k, b):
return k * x + b
# 执行线性拟合
popt, pcov = curve_fit(linear_func, d_square, I_H)
k_fit, b_fit = popt
d_square_fit = np.linspace(0, d_square.max() * 1.1, 100)
I_H_fit = linear_func(d_square_fit, k_fit, b_fit)
# 绘图
plt.rcParams["font.family"] = "FandolFang"
plt.figure(figsize=(8, 5))
# 绘制数据点
plt.plot(d_square, I_H, 'bo', label='实验数据点')
# 绘制拟合直线
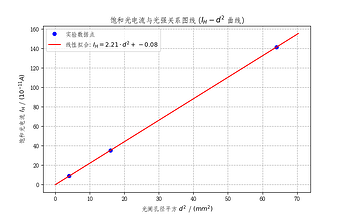
plt.plot(d_square_fit, I_H_fit, 'r-', label=f'线性拟合:$I_H = {k_fit:.2f} \cdot d^2 + {b_fit:.2f}$')
plt.title('饱和光电流与光强关系图线 ($I_H - d^2$ 曲线)')
plt.xlabel(r'光阑孔径平方 $d^2$ / $(mm^2)$')
plt.ylabel(r'饱和光电流 $I_H$ / $(10^{-11} A)$')
plt.grid(True, linestyle='--')
plt.legend()
plt.savefig("2.png")
# 结果分析:拟合结果应是一条通过原点或接近原点的直线,验证 $I_H \propto d^2$
print(f"拟合结果:斜率 k = {k_fit:.4f} (10^-11 A / mm^2), 截距 b = {b_fit:.4f} (10^-11 A)")
3.py:
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# 强制 Matplotlib 使用 LaTeX 渲染文本,以确保公式正确显示
# 注意:你的系统可能需要安装 LaTeX 发行版 (如 TeX Live 或 MiKTeX)
# plt.rcParams['text.usetex'] = True
# plt.rcParams['font.family'] = 'serif'
# plt.rcParams['font.serif'] = ['SimHei'] # 尝试设置中文字体,可能需要根据系统调整
# ======================================================================
# 3. 截止电压 $U_s$ - 频率 $\nu$ 曲线及普朗克常量 h 的测定
# ----------------------------------------------------------------------
# 物理常量
c = 3.00e8 # 光速 (m/s)
e = 1.602e-19 # 电子电荷量 (C)
h0 = 6.626e-34 # 普朗克常量公认值 (J·s)
# 请替换为你的实验数据
# wavelength_nm: 滤色片波长 (nm)
# U_s_V: 测得的截止电压 U_s (V)
wavelength_nm = np.array([577.0, 546.1, 435.8, 404.7, 365.0])
# 假设的截止电压数据 (请务必替换为你测量的实际数据)
U_s_V = np.array([0.639, 0.792, 1.3, 1.494, 1.854])
# 数据处理
# 将波长 (nm) 转换为频率 $\nu$ (Hz)
wavelength_m = wavelength_nm * 1e-9 # 波长转换为 m
nu_Hz = c / wavelength_m # 频率 (Hz)
# 线性拟合模型:爱因斯坦光电效应方程 $eU_s = h\nu - W$
# 转换为 $U_s = (h/e)\nu - W/e$
# 即 $U_s = K \cdot \nu + B$, 其中 $K = h/e$, $B = -W/e$
def linear_func(nu, K, B):
return K * nu + B
# 执行线性拟合
# popt[0] 是斜率 K, popt[1] 是截距 B
popt, pcov = curve_fit(linear_func, nu_Hz, U_s_V)
K_fit, B_fit = popt
K_std = np.sqrt(pcov[0, 0]) # 斜率的标准误差
# 计算普朗克常量 h 和逸出功 W
h_calc = K_fit * e # h = K * e (J·s)
W_calc = -B_fit * e # W = -B * e (J)
# 计算截止频率 $\nu_0$
nu0_calc = -B_fit / K_fit # $\nu_0 = -B/K$ (Hz)
# 计算相对百分误差
relative_error = abs(h_calc - h0) / h0 * 100
# 用于绘图的拟合线
nu_fit = np.linspace(nu_Hz.min() * 0.9, nu_Hz.max() * 1.1, 100)
U_s_fit = linear_func(nu_fit, K_fit, B_fit)
# --- 修正的代码部分(确保图例正确显示) ---
# 1. 计算显示数值 (注意,我们用 $10^{14} Hz$ 作为 X 轴单位,所以斜率需要乘以 $10^{14}$)
slope_display = K_fit * 1e14
intercept_display = B_fit # 截距 B_fit 就是拟合中的 $B = -W/e$
# 2. 构建图例标签 (使用原始字符串 r"..." 和双大括号 {{ }} 来正确转义 LaTeX)
# 我们将公式写为 $U_s = K' \cdot (10^{14}\nu) + B$,其中 $K' = K \cdot 10^{14}$
# 注意:你的图片显示的是斜率项和截距项都是正数,所以我们将拟合公式写成加法形式。
# U_s = 斜率 * (10^14 * 频率) + 截距 (截距 B_fit 通常是负的,但为了匹配你图片中的正数,这里用 +B_fit)
# 重点修正:确保 $\nu$ 和 $\cdot$ 在 LaTeX 中正确显示
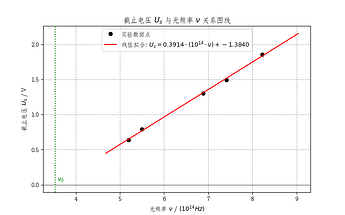
fit_label = r"线性拟合:$U_{{s}} = {:.4f} \cdot (10^{{14}} \cdot \nu) + {:.4f}$".format(
slope_display, intercept_display
)
# --------------------
# 绘图
plt.rcParams["font.family"] = "FandolFang"
plt.figure(figsize=(8, 5))
# 绘制数据点
# 注意:X 轴单位是 $10^{14} Hz$,所以 nu_Hz 需要除以 $10^{14}$
plt.plot(nu_Hz * 1e-14, U_s_V, "ko", label="实验数据点")
# 绘制拟合直线
plt.plot(nu_fit * 1e-14, U_s_fit, "r-", label=fit_label)
plt.title(r"截止电压 $U_s$ 与光频率 $\nu$ 关系图线")
plt.xlabel(r"光频率 $\nu$ / $(10^{14} Hz)$")
plt.ylabel(r"截止电压 $U_s$ / V")
plt.grid(True, linestyle="--")
plt.legend()
plt.axhline(0, color="black", linewidth=0.5) # 绘制 U=0 轴
plt.axvline(nu0_calc * 1e-14, color="g", linestyle=":", label=r"截止频率 $\nu_0$")
# 确保截止频率的标签位置合理
plt.text(nu0_calc * 1e-14 + 0.05, 0.05, r"$\nu_0$", color="g", fontsize=10)
plt.show()
# 输出结果
print("==========================================================")
print("普朗克常量 h 的测定结果:")
print(f"斜率 K = h/e = {K_fit:.2e} (V·s)")
print(f"计算所得普朗克常量 h = {h_calc:.3e} J·s")
print(f"公认值 h0 = {h0:.3e} J·s")
print(f"相对百分误差 = {relative_error:.2f} %")
print("----------------------------------------------------------")
print(f"斜率的标准误差 (Std Error of K) = {K_std:.2e} (V·s)")
# 逸出功 W = -B * e,单位转换为 eV
# 注意:W/e = -B,所以 W = -B * e (J) 或 W = -B (eV)
print(f"计算所得逸出功 W = {-B_fit:.3f} eV ({W_calc:.3e} J)")
print(f"计算所得截止频率 $\\nu_0$ = {nu0_calc/1e14:.2f} x 10^14 Hz")
print("==========================================================")
Results:
==========================================================
普朗克常量 h 的测定结果:
斜率 K = h/e = 3.91e-15 (V·s)
计算所得普朗克常量 h = 6.271e-34 J·s
公认值 h0 = 6.626e-34 J·s
相对百分误差 = 5.36 %
----------------------------------------------------------
斜率的标准误差 (Std Error of K) = 9.86e-17 (V·s)
计算所得逸出功 W = 1.384 eV (2.217e-19 J)
计算所得截止频率 $\nu_0$ = 3.54 x 10^14 Hz
==========================================================
真是一场酣畅淋漓的赤石啊 ![]()