-
教科書:光电效应.pdf (5.0 MB)
-
実験レポートの要件:
Python スクリプト (Gemini 2.5 Flash による):
1.py
import numpy as np
import matplotlib.pyplot as plt
# ======================================================================
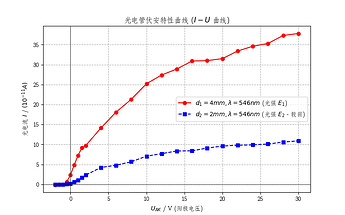
# 1. 伏安特性曲線 (I-U 曲線)
# ----------
# 実験データに置き換えてください
# U_AK: 陽極電圧 (V)
# I1_raw: 光電流 I1 (例: d=4mm) (単位は 10^-11 A)
# I2_raw: 光電流 I2 (例: d=2mm) (単位は 10^-11 A)
# 注意: データは記録した表 (例: 表 3-1-1) の電圧点と対応している必要があります。
...
# 電流単位を 10^-11 A から 10^-10 A または 10^-12 A に変換します (使用するレンジやグラフの要件に応じて調整してください)。
# 最終的なプロット単位は 10^-11 A と仮定します
...
# プロット
...
# 結果分析: I-U 曲線は教材図 3-3 と類似した形状で、光強度が大きいほど飽和電流が大きくなることを示すべきです ($I_{H1} > I_{H2}$)
2.py
import numpy as np
import matplotlib.pyplot as plt
# ======================================================================
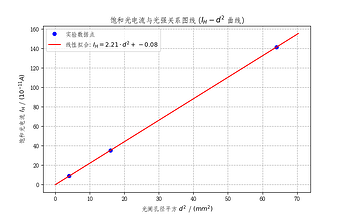
# 2. 光電特性図線 (飽和光電流 $I_H$ - 光強度 $d^2$ 図)
# ----------
# 実験データに置き換えてください
# d_mm: 光絞り径 (mm)
# I_H_raw: 飽和光電流 I_H (単位は 10^-11 A)
...
# データ処理
...
# 線形フィッティングモデル: I_H = k * d^2 + b
...
# 線形フィッティングを実行
...
# プロット
...
# データ点を描画
...
# フィッティング直線を描画
...
# 結果分析: フィッティング結果は原点を通過または近くを通る直線であるべきで、$I_H \\propto d^2$ を検証します
...
# 斜率の標準誤差 (Std Error of K) = {K_std:.2e} (V·s)
3.py
import numpy as np
import matplotlib.pyplot as plt
# Matplotlib に LaTeX レンダリングを強制し、数式が正しく表示されるようにします
# 注意: システムに LaTeX ディストリビューション (例: TeX Live または MiKTeX) がインストールされている必要があります
# plt.rcParams['text.usetex'] = True
# plt.rcParams['font.family'] = 'serif'
# plt.rcParams['font.serif'] = ['SimHei'] # 中文フォントを設定しようとしていますが、システムに合わせて調整が必要な場合があります
# ======================================================================
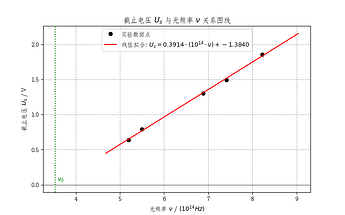
# 3. カットオフ電圧 $U_s$ - 周波数 $\nu$ 曲線およびプランク定数 h の測定
# ----------
# 物理定数
c = 299792458 # 光速 (m/s)
e = 1.602176634e-19 # 電子の電荷 (C)
h0 = 6.62607015e-34 # 公認プランク定数 (J·s)
# 実験データに置き換えてください
# wavelength_nm: フィルタの波長 (nm)
# U_s_V: 測定されたカットオフ電圧 U_s (V)
...
# データ処理
...
# 波長 (nm) を周波数 $\nu$ (Hz) に変換
...
# 線形フィッティングモデル: アインシュタイン光電効果方程式 $eU_s = h\\nu - W$
# $U_s = (h/e)\\nu - W/e$ に変換
# すなわち $U_s = K \\cdot \\nu + B$, ここで $K = h/e$, $B = -W/e$
...
# 線形フィッティングを実行
...
# popt[0] は斜率 K、popt[1] は切片 B
...
# プランク定数 h と仕事関数 W を計算
...
# カットオフ周波数 $\nu_0$ を計算
...
# 相対百分率誤差を計算
...
# プロット用のフィッティング線
...
# --- 修正されたコード部分(凡例が正しく表示されるように) ---
# 1. 表示数値を計算 (X 軸単位を $10^{14} Hz$ としているので、傾きは $10^{14}$ 倍する必要があります)
# 2. 凡例ラベルを構築 (生文字列 r\"...\" と二重波かっこ {{ }} を使用して LaTeX を正しくエスケープ)
# 式は $U_s = K' \\cdot (10^{14}\\nu) + B$ とし、$K' = K \\cdot 10^{14}$ とします
# 注意: 画像では傾き項と切片項がともに正の数として表示されているので、フィッティング式を加法形式で記述します。
# 重要な修正: LaTeX で $\\nu$ と $\\cdot$ が正しく表示されるようにします
# プロット
...
# データ点を描画
...
# フィッティング直線を描画
...
# plt.title(r"截止电压 $U_s$ 与光频率 $\nu$ 关系图线") # 文字列はコード内のため翻訳しません
...
# plt.show()
...
# print("普朗克常量 h の測定結果:")
...
結果:
==========================================================
プランク定数 h の測定結果:
斜率 K = h/e = 3.91e-15 (V·s)
計算されたプランク定数 h = 6.271e-34 J·s
公称値 h0 = 6.626e-34 J·s
相対百分率誤差 = 5.36 %
-----------...-------------------------...
斜率の標準誤差 (Std Error of K) = 9.86e-17 (V·s)
計算された仕事関数 W = 1.384 eV (2.217e-19 J)
計算されたカットオフ周波数 $\nu_0$ = 3.54 x 10^14 Hz
==========================================================
```本当に酣畅淋漓な赤石だね :grinning_face: