课程:PHYS316509-量子力学
教材:张盈 量子力学基本原理 [M] 西安:西安交通大学出版社,2023
教师:张盈
学分:5.0
授课学时:80.0
开课单位:物理学院
考试类型:闭卷
- 大三上开课。
- 成绩构成:平时 30%、期中 30%、期末 40%。平时成绩由随堂测试、作业、讨论等构成。
- 安排 3 次随堂测试,2 次电子作业。
- zy 老师上课重概念理解,轻数学运算,授课时常结合高能物理应用。
- 作业很少,部分题有难度。
- 本科生只学习初量。
读书心得
学习量子力学时,应广泛阅读和对比不同书籍。下面对读过的部分书做一评论。
个人钟情曾谨言的书,行文如其名,论述严谨,语言简明,既有深度,又有广度,写得十分标准,是国内经典教科书。卷一大致对应初等量子力学部分,卷二大致对应高等量子力学部分。学习时只挑拣需要的章节阅读即可。后续可以作为字典时时回顾。
对于初等量子力学:
- Griffith 的《量子力学概论》行文流畅,最为易懂,是国外经典教科书。用最简单的语言讲出最深刻的原理,数学推导详尽,物理图像清晰,部分习题经典。初次学习阅读是比较好的。
- 田光善的量子力学讲义大致以曾书为框架,编写完善,推导更详细,论述更清晰。配以 B 站网课,个人尤其推荐表象变换和对称性的部分,讲授非常清晰,无出其右。
- zy 的这本《量子力学基本原理》是一本新书,有些许错讹,基本原理部分的论述很清楚,有一些地方的数学处理不清楚。听说这本书是为下一届准备的,到那时这门课的学时就改为了 64 学时,所以书中不包含变分法和 WKB 近似部分。总体来说内容比较全面,但不是非常深入。
对于高等量子力学:
- Sakurai 的《现代量子力学》结构完善,难度不算大,用作从初等向高等的过渡很合适。个人感觉稍啰嗦一点,看得不多。
- 田光善的高等量子力学讲义大致以曾书为框架,给出了最为详细的数学推导和各种数学技巧,尤其是二次量子化和角动量理论部分,后面群论在量子力学中的应用同样深入浅出,重点突出,最为实用。
- 喀兴林的《高等量子力学》比较老,但是论述得比较清晰且细致,尤其是散射和二次量子化部分,有不懂的可以来看一下。
- 闫学群的《高等量子力学》不同于传统高量教材,侧重于量子光学和量子信息,对量子纠缠、量子测量、量子开放系统理论进行了详细的论述,简明而实用。
对于量子光学:
- Scully 的《量子光学》是最经典的教材,结构清晰,最为标准。
- 郭光灿的《量子光学》有更多的数学推导,内容更丰富些,但是有些地方跳跃性较大。应注意本书对压缩态的定义不同于 Scully,并且对量子分布理论的论述较少。
以上仁者见仁,智者见智。
2025.1.5 期末考试回忆
一、简答题(6×8=48)
- 简述使用量子力学原理讨论氢分子稳定性的思路。
- WKB 近似的适用条件为何?写出非经典区域中波函数的形式。
- Born 近似和 Lippmann-Schwinger 方程的关系是什么?写出 Born 近似散射振幅的表达式。
- 从 Schrodinger 方程出发推导 Lippmann-Schwinger 方程。
- 用非简并微扰论处理简并微扰论的困难何在?正确的做法是什么?
- 简述使用半经典近似处理光的受激吸收和辐射的思路。“半经典”是什么意思?
- 简述厄米算符的性质和可观测物理量的性质之间的对应关系。
- 分波法中相移 \delta_l 的物理意义是什么(是什么波的相位移动)?
二、计算题(52)
- 从一维无限深方势阱出发,推导:(12)
- 能量本征波函数;
- 能级;
- 粒子运动的含时波函数。
-
推导非简并微扰论的能量一级修正和波函数一级修正公式。(12)
-
计算下面 Heisenberg 绘景中算符的时间演化 \frac{\mathrm{d}}{\mathrm{d}t}\hat{A}_H(t) :(12)
\hat{A}_H(t) = \mathrm{e}^{\frac{\mathrm{i}}{\hbar}\hat{H}t}\hat{A}_S\mathrm{e}^{-\frac{\mathrm{i}}{\hbar}\hat{H}t}
- 根据谐振子产生湮灭算符的定义:(16)
\hat{a}^\dagger = \frac{1}{\sqrt{2\hbar m\omega}}(m\omega\hat{x} - \mathrm{i}\hat{p}),\quad \hat{a} = \frac{1}{\sqrt{2\hbar m\omega}}(m\omega\hat{x} + \mathrm{i}\hat{p})
- 计算对易关系 [\hat{a},\hat{a}^\dagger],\ [\hat{H},\hat{a}],\ [\hat{H},\hat{a}^\dagger],说明 \hat{a}|n\rangle 和 \hat{a}^\dagger|n\rangle 的物理意义;
- 证明:
\hat{a}|n\rangle = \sqrt{n}|n-1\rangle,\quad
\hat{a}^\dagger|n\rangle = \sqrt{n+1}|n+1\rangle
- 计算:
\hat{x}|n\rangle,\quad
\hat{p}|n\rangle
- 计算第 n 激发态的位置不确定度和动量不确定度,验证不确定关系。
试题简评
简单,注重物理理解。简答题要求对细节足够熟悉。计算题白给。
量子力学笔记
Quantum_Mechanics.pdf (1.1 MB)
1-10 章大致对应初量,11-17 章大致对应高量,18-23 章大致对应量光。
本笔记为第一版,有些内容未涉及,如路径积分、相对论量子力学等。
电子作业
一、自由粒子波函数的演化
clear; close all; clc;
hbar = 1;
m = 1;
a = 1;
L = 100; % 积分限
N_x = 400; % x 采样数
N_t = 200; % t 采样数
x_min = -10;
x_max = 10;
t_min = 0;
t_max = 5;
% 定义空间和时间范围
x_values = linspace(x_min, x_max, N_x);
t_values = linspace(t_min, t_max, N_t);
% 预分配模方数组
psi_square = zeros(N_x, N_t);
% MATLAB 的 integral 函数无法直接处理复数,分开处理实部和虚部
integrand_r = @(k, x, t) (1/sqrt(pi*a)) .* (sin(k*a) ./ k) .* cos(k*x - (hbar*k.^2/(2*m)) * t);
integrand_i = @(k, x, t) (1/sqrt(pi*a)) .* (sin(k*a) ./ k) .* sin(k*x - (hbar*k.^2/(2*m)) * t);
% 循环计算每个时间点的波函数模方
for ti = 1 : N_t
t = t_values(ti);
fprintf('计算时间点 t = %.3f / %.3f\n', t, t_max);
% 对每个 x 计算积分
for xi = 1 : N_x
x = x_values(xi);
Re = integral(@(k) integrand_r(k, x, t), -L, L, 'AbsTol',1e-10,'RelTol',1e-8);
Im = integral(@(k) integrand_i(k, x, t), -L, L, 'AbsTol',1e-10,'RelTol',1e-8);
psi = (1/sqrt(2*pi)) * (Re + 1i*Im);
psi_square(xi, ti) = abs(psi)^2;
end
end
% 创建动画
figure;
h = plot(x_values, psi_square(:,1), 'b', 'LineWidth', 2);
xlabel('x');
ylabel('|\psi(x,t)|^2');
title('Time Evolution of Free Patical');
grid on;
ylim([0, max(psi_square(:)) * 1.1]); % 动态调整 y 轴范围
% 初始化视频写入对象
v = VideoWriter('wave_function_evolution.mp4','MPEG-4');
v.FrameRate = 30; % 设置帧率
open(v);
% 循环生成每一帧
for ti = 1:N_t
set(h, 'YData', psi_square(:,ti));
title(sprintf('Time Evolution of Free Patical (t = %.2f)', t_values(ti)));
drawnow;
% 捕获当前帧
frame = getframe(gcf);
writeVideo(v, frame);
end
% 关闭视频写入对象
close(v);
disp('动画已保存为 wave_function_evolution.mp4');
% 播放生成的视频
implay('wave_function_evolution.mp4');
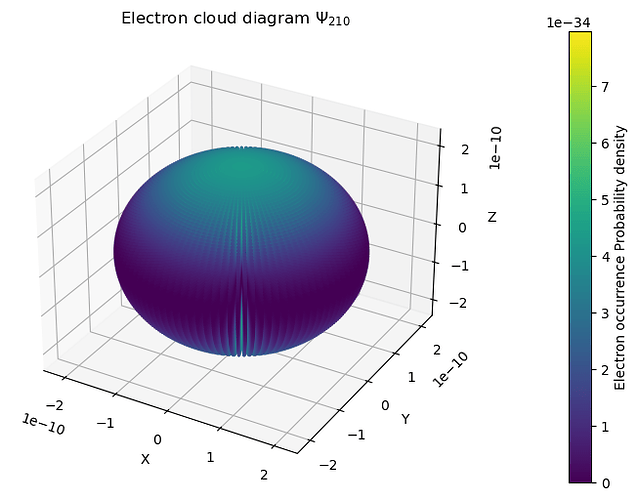
二:氢原子 |\psi_{210}(r,\theta,\varphi)|^2 染色
R_{21}(r) = \frac{1}{a\sqrt{6}a^{3/2}}\frac{r}{a}\mathrm{e}^{-\frac{r}{2a}}
Y_{10}(\theta,\varphi) = \sqrt{\frac{3}{4\pi}}\cos{\theta}
\psi_{210}(r,\theta,\varphi) = R_{21}(r)Y_{10} = \frac{1}{4\sqrt{2\pi}a^{3/2}}\frac{r}{a}\mathrm{e}^{-\frac{r}{2a}}\cos{\theta}
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Bhor 半径
a = 5.29e-11 # 单位:米
# 球坐标网格
r = np.linspace(0, 4 * a, 100) # 径向距离(单位:米)
theta = np.linspace(0, np.pi, 100) # 极角范围 0 到 pi
phi = np.linspace(0, 2 * np.pi, 100) # 方位角范围 0 到 2pi
# 网格化
r, theta, phi = np.meshgrid(r, theta, phi)
# 波函数模方 |\Psi_{210}(r, θ, φ)|^2
psi_square = (1 / (32 * np.pi) * a**3) * (r**2 / a**2) * np.exp(-r / a) * np.cos(theta)**2
# 转换为直角坐标系
x = r * np.sin(theta) * np.cos(phi)
y = r * np.sin(theta) * np.sin(phi)
z = r * np.cos(theta)
# 绘制三维图
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
# 使用概率密度值来设定颜色
sc = ax.scatter(x, y, z, c=psi_square, cmap='viridis', marker='o', s=1)
# 添加颜色条
cbar = fig.colorbar(sc, ax=ax, pad=0.1)
cbar.set_label("Electron occurrence Probability density")
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Electron cloud diagram $\Psi_{210}$')
# 调整布局,避免颜色条挡住标签
fig.subplots_adjust(right=1.5)
# 显示图像
plt.show()
为了方便观察,只选择大于 0.6 倍最大概率的部分进行染色,如下图。与教科书上图形一致。
# 设置阈值:选择最大概率密度的某个百分比作为阈值
threshold = 0.6
max_psi_square = np.max(psi_square)
mask = psi_square > threshold * max_psi_square
# 提取符合条件的 x, y, z 坐标
x = r[mask] * np.sin(theta[mask]) * np.cos(phi[mask])
y = r[mask] * np.sin(theta[mask]) * np.sin(phi[mask])
z = r[mask] * np.cos(theta[mask])
# 获取颜色条的 vmin 和 vmax,用于确保两幅图使用相同的颜色映射范围
vmin = np.min(psi_square)
vmax = np.max(psi_square)
# 创建第二幅图:显示阈值筛选后的电子云
fig2 = plt.figure(figsize=(8, 6))
ax2 = fig2.add_subplot(111, projection='3d')
sc2 = ax2.scatter(x, y, z, c=psi_square[mask], cmap='viridis', marker='o', s=1, vmin=vmin, vmax=vmax)
# 设置颜色条范围与第一幅图相同
cbar2 = fig2.colorbar(sc2, ax=ax2, pad=0.1)
cbar2.set_label("Electron occurrence Probability density")
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')
ax2.set_title('Electron cloud diagram $\Psi_{210}$ (Thresholded)')
# 显示图像
plt.show()
真是神清气爽![]()