不难的,放心~只要有的聊就好 ![]()
下周二一面,二面也没有算法吗,对面告诉我好像是写 rust + ai infra
算法最好也准备一下,有备无患,我是两次面试都没叫手撕算法,而且已经拿到 offer 啦 ![]()
下午要把 leetcode 刷了,一日无 coding 则手生,两日无 coding 则手废矣,等到天晴了再出去玩一天 ![]()
下周二二面,啊~~~~好累
2025 年 6 月 13 日 星期五 天气:小雨
上午抱佛脚![]() 面试 记录 | 大学里的最后一段时光 #日记楼 - #119,来自 sumire
面试 记录 | 大学里的最后一段时光 #日记楼 - #119,来自 sumire
中午摸鱼 1 个半小时 ![]()
下午学长又要求开会,给我们安排了新的任务,不想再看论文 + 想负载均衡算法了,累
晚上做题非常不顺手,首先每日一题就给我暴击
二分 + 贪心,这种题目就是专门增加调试时间 + 卡贪心考虑不足的 QAQ
C++
class Solution {
public:
int minimizeMax(vector<int>& nums, int p) {
sort(nums.begin(), nums.end());
auto check = [&](int mx) -> bool {
int cnt = 0;
for(int i = 0; i < nums.size() - 1; i++) {
if(nums[i+1]-nums[i] <= mx) {
cnt++;
i++;
}
}
return cnt >= p;
};
int left = 0, right = nums.back() - nums[0];
while (left < right) {
int mid = (left + right) >> 1;
if (check(mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
};
然后战一些很奇怪的网格图 dijkstra。
这题可以用并查集,也可以用 dijkstra。并查集的思路就像水逐渐淹过去一样,建立一个高度 → 索引的映射即可,这里直接用 vector 就好。直到某个时刻起点和终点相互连接。
C++
class Union {
public:
vector<int> parents;
vector<int> size;
int n;
Union(int n):n(n), parents(vector<int>(n)), size(vector<int>(n, 1)) {
iota(parents.begin(), parents.end(), 0);
}
int find(int id) {
if(parents[id] != id) {
return find(parents[id]);
}
return id;
}
void merge(int id1, int id2) {
int pa1, pa2;
pa1 = find(id1), pa2 = find(id2);
if(pa1 == pa2) return;
else if(size[pa1] < size[pa2]) {
parents[pa1] = pa2;
size[pa2] += size[pa1];
} else {
parents[pa2] = pa1;
size[pa1] += size[pa2];
}
}
};
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> indices(m*n); // Tips: No repeat.
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
indices[grid[i][j]] = i*m+j;
}
}
constexpr int dir[4][2] = {{-1, 0},{1, 0},{0, -1},{0, 1}};
Union u(m*n);
// Merge.
int t;
for(t = 0; t < m*n; t++) {
int cur = indices[t];
int cur_i, cur_j;
cur_i = cur / m, cur_j = cur % m;
for(int i = 0; i < 4; i++) {
int new_i = cur_i + dir[i][0], new_j = cur_j + dir[i][1];
if(new_i >= 0 && new_i < m && new_j >= 0 && new_j < n) {
int adj_height = grid[new_i][new_j];
if(adj_height <= t) {
u.merge(cur, new_i * m + new_j);
}
}
}
if(u.find(0) == u.find(m*n - 1)) {
break;
}
}
return t;
}
};
dijkstra 算法就是网格图,不需要建图(会导致非常稠密浪费时间和空间)。
C++
// The Dijkstra algorithm.
constexpr int directions[4][2] = {{-1, 0},{1, 0},{0, -1},{0, 1}};
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int N = m * n;
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
vector<int> distance(N, INT_MAX);
distance[0] = grid[0][0];
pq.emplace(distance[0],0);
while(!pq.empty()) {
const auto [dist, cur] = pq.top();
pq.pop();
if(dist > distance[cur]) continue;
// Coordinate decomposition. cur = i * m + j.
int cur_i = cur / m, cur_j = cur % m;
for(int i = 0; i < 4; i++) {
int adj_i = cur_i + directions[i][0];
int adj_j = cur_j + directions[i][1];
int adj = adj_i * m + adj_j;
if(adj_i >= 0 && adj_i < m && adj_j >= 0 && adj_j < n) {
int new_dist = max(dist, grid[adj_i][adj_j]);
if(distance[adj] > new_dist) {
distance[adj] = new_dist;
pq.emplace(distance[adj], adj);
}
}
}
}
return distance[N - 1];
}
};
目前还想不出来,明天再战(对不起 ldx 想睡觉 ![]() )
)
主要的想法就是这题目比较复杂,我们需要了解到,这样一个稠密图我们只需要计算需要进行计算的邻边。我们的目标是 start → target,因此第一条邻边就是两者之间的曼哈屯距离~
接下来需要考虑的是特殊边。我们看下图就明白应该执行怎样的“松弛操作”(算法导论中的术语)
主要是不能晕掉,牢靠把握 dijkstra 的流程:
寻找起点的邻边 → 进行松弛操作 → 更新则加入队列 → 对新的邻边进行松弛操作 → 直到终点为止。图中就是分别对 j 进行了邻边 i 的松弛操作,对 n-1 进行了 j 的松弛操作。
然后就是防止内存爆炸 10^5\times 10^5 需要对 (x,y) 进行编码操作。这里编码采用 (x << 32)|y ,解码采用 x = key >> 32, y = key & ((1ll << 32) - 1) 的方式进行。
C++
using ll = long long;
constexpr ll MASK = (1ll << 32) - 1;
class Solution {
public:
ll coord2Key(int i, int j) {
ll key = ((ll)i << 32) | j;
return key;
}
pair<int,int> key2Coord(ll key) {
int i = key >> 32;
int j = key & MASK;
return make_pair(i, j);
}
int minimumCost(vector<int>& start, vector<int>& target, vector<vector<int>>& specialRoads) {
priority_queue<pair<ll,ll>, vector<pair<ll,ll>>, greater<pair<ll,ll>>> pq;
unordered_set<ll> visited;
unordered_map<ll, ll> distance;
int start_x = start[0], start_y = start[1];
int target_x = target[0], target_y = target[1];
ll s = coord2Key(start_x, start_y), t = coord2Key(target_x, target_y);
distance[s] = 0;
pq.emplace(0, s);
while(!pq.empty()) {
const auto [dist, cur] = pq.top();
pq.pop();
if(cur == t) break;
if(visited.find(cur) != visited.end()) continue;
visited.insert(cur);
// Update current point to target.
const auto & [cur_x, cur_y] = key2Coord(cur);
if(distance.find(t) == distance.end() || distance[t] > dist + llabs(cur_x - target_x) + llabs(cur_y - target_y)) {
distance[t] = dist + llabs(cur_x - target_x) + llabs(cur_y - target_y);
pq.emplace(distance[t], t);
}
// Update the special roads' ends. start -> cur --- (sp.road) ---> end;
for(const auto & roads: specialRoads) {
ll new_dist = dist + (ll)abs(roads[0] - cur_x) + (ll)abs(roads[1] - cur_y) + roads[4];
ll adj = coord2Key(roads[2], roads[3]);
if(distance.find(adj) == distance.end() || new_dist < distance[adj]) {
distance[adj] = new_dist;
pq.emplace(distance[adj],adj);
}
}
}
return distance[t];
}
};
祝各位晚安~
写累了,稍微总结一下今天写的题目
乍一看没反应过来这怎么用 dijkstra 做,稍微看了看提示,原来是当 x\to y 成立的时候,将边权设立为 y 即可。
判断质数采用埃氏筛即可。这一部分预处理完成。
C++
constexpr int MAXN = 1e4+5;
bool notPrime[MAXN]; // When not prime, mark true.
// Eratosthenes prime number calculation.
int init = []() -> int {
notPrime[0] = true, notPrime[1] = true;
for(int i = 2; i < MAXN; i++) {
if(notPrime[i] == false) {
for(int j = i * i; j < MAXN; j += i) {
notPrime[j] = true;
}
}
}
return 0;
}(); // found all prime number.
auto length = [](int num) -> int {
int len = 0;
while(num) {
num /= 10;
len++;
}
return len;
};
class Solution {
public:
int minOperations(int n, int m) {
if(notPrime[n] == false || notPrime[m] == false) {
return -1;
}
int len_n = length(n);
vector<int> distance(pow(10, len_n), INT_MAX);
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
pq.emplace(n, n);
while(!pq.empty()) {
const auto [dist, cur] = pq.top();
pq.pop();
if(cur == m) return dist;
if(dist > distance[cur]) continue;
int ratio = 1;
for(int digit = cur; digit > 0; digit /= 10) {
if(digit % 10 < 9) {
int adj = cur + ratio;
if(notPrime[adj] && distance[adj] > dist + adj) {
distance[adj] = dist + adj;
pq.emplace(distance[adj],adj);
}
}
if(digit % 10 > 0) {
int adj = cur - ratio;
if(notPrime[adj] && distance[adj] > dist + adj) {
distance[adj] = dist + adj;
pq.emplace(distance[adj],adj);
}
}
ratio *= 10;
}
}
return -1;
}
};
换一些思路做一下 dp
dfs(i,j)=grid[i][j]+\min_{k=0}^{n-1}dfs(i+1,k)+moveCost[grid[i][j][k]]
这样我们的转移就是在 i 上倒序进行的,并且可以优化成两个一维数组。
C++
class Solution {
public:
int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {
int m = grid.size();
int n = grid[0].size();
// vector<vector<int>> dp = vector<vector<int>>(m, vector<int>(n,0));
int * dp_old = new int [n];
int * dp_new = new int [n];
for(int j = 0; j < n; j++) {
dp_old[j]= grid[0][j];
dp_new[j] = dp_old[j];
}
int ans = INT_MAX / 2;
for(int i = 1; i < m; i++) {
for(int j = 0; j < n; j++) {
int temp = INT_MAX / 2;
for(int k = 0; k < n; k++) {
temp = min(temp, dp_old[k]+moveCost[grid[i-1][k]][j]);
}
dp_new[j] = temp + grid[i][j];
if(i == m-1) ans = min(ans, dp_new[j]);
}
int * temp = dp_old;
dp_old = dp_new;
dp_new = temp;
}
return ans;
}
};
这一题采用记忆化的 dfs 方法来进行。因为我们有重复的分支,因此将其记录下来防止指数级别增长即可。
C++
constexpr int directions[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; // Directions in four ways, RLUD.
class Solution {
vector<vector<int>> memo;
int m;
int n;
public:
int dfs(int x, int y, vector<vector<int>> & mat) {
if(memo[x][y] != -1) return memo[x][y]; // Prune the dfs branch.
memo[x][y] = 1; // Initial value with 1.
for(int i = 0; i < 4; i++) {
int nx = x + directions[i][0], ny = y + directions[i][1];
if(nx >= 0 && nx < m
&& ny >= 0 && ny < n
&& mat[nx][ny] > mat[x][y]) {
memo[x][y] = max(dfs(nx, ny, mat) + 1, memo[x][y]);
}
}
return memo[x][y];
}
int longestIncreasingPath(vector<vector<int>>& matrix) {
m = matrix.size();
n = matrix[0].size();
// Abnormal situation dealing with m,n has 0.
if(m == 0 || n == 0) {
return 0;
}
memo = vector<vector<int>>(m, vector<int>(n,-1));
int ans = INT_MIN / 2;
// DFS started at each coord.
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
ans = max(dfs(i,j,matrix),ans);
}
}
return ans;
}
};
思考:dijkstra 与 dp 的区别?
一般来说在图上进行 dp 的时候需要保证无后效型。即后面更新的动作无法影响到已经更新完成的部分。而 dijkstra 算法具有松弛操作,会根据后面点的更新而影响前者(因为后面更新的节点会加入到队列中,从而回过头来可能更新原先遍历过的点)。因此需要观察是否更新无后效型。
今天好热啊下午又闷又热让アイラちゃん做题进展缓慢 ![]()
不学了今晚摸鱼 ![]()
周末要休息一下 ![]()
进行一个赛博吸猫 ![]()
好乖的小猫![]()
不知道为什么我看这两小只很像两块砖头![]()
![]()
猫猫砖可爱捏
小结一下然后学一下数学~
暴力即可。
C++
class Solution {
public:
int maxDiff(int num) {
string s = to_string(num);
string original = s;
int minNum = INT_MAX, maxNum = INT_MIN;
for(int x = 0; x <= 9; x++) {
for(int y = 0; y <= 9; y++) {
for(int i = 0; i < s.length(); i++) {
if(s[i] == '0' + x) {
s[i] = '0' + y;
}
}
if(s[0] != '0' && stoi(s) != 0) {
minNum = min(stoi(s), minNum);
maxNum = max(stoi(s), maxNum);
}
s = original;
}
}
return maxNum - minNum;
}
};
对于 Dijkstra 进行更深一步的考察。对于最短路我们每次都需要进行一次松弛操作,于是对于那些比最短路更长一点的第二短路径也进行松弛操作即可。需要注意的是这里的边是无权边(具有相同权重的边也可以视为无权边),就可以采用普通的 queue 进行松弛操作。
C++
// Using BFS to find the shortest path with the second shortest path.
class Solution {
public:
int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {
// Step 1: Build graph here.
vector<vector<int>> graph(n+1);
for(const auto edge: edges) {
int u = edge[0], v = edge[1];
graph[u].emplace_back(v);
graph[v].emplace_back(u);
}
// Step 2: function that get the next time.
auto step = [&](int curTime) -> int {
int round = curTime / change; // Whether it is green or not. % 2 == 0: green;
if(round % 2 == 1) {
return (round + 1) * change + time; // next green light + edge weight.
}
return curTime + time;
};
// Step 3: BFS for 0-1 shortest path.
vector<vector<int>> distance(2, vector<int>(n+1, INT_MAX)); // distance[0] -> shortest;
queue<pair<int,int>> q; // 0-1 BFS using queue is OK;
q.emplace(0, 1);
distance[0][1] = 0;
while(!q.empty()) {
const auto [dist, cur] = q.front();
q.pop();
for(const auto & adj: graph[cur]) {
int next_time = step(dist); // Calculate new time.
if(distance[0][adj] > next_time) {
distance[0][adj] = next_time;
q.emplace(next_time, adj);
} else if(distance[0][adj] < next_time && distance[1][adj] > next_time) {
distance[1][adj] = next_time;
q.emplace(next_time, adj);
}
}
}
return distance[1][n];
}
};
看到最大中找最小其实第一反应是二分。于是可以进行 dfs 判断访问其他点,从而获得最大值,二分获得目标之下的最大值。但是此时假设边权最大为 U,如果边权很大将会被卡掉时间复杂度 E\log{U} 。我们可以看到边权最大值是 10^6, 但是反向建图+dijkstra 的时间复杂度是 m\log{m}, 所以我们选择 dijkstra 即可。
只需要计算出来所有距离的最大值即可。
C++
using pii = pair<int,int>;
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
if (edges.size() < n - 1) {
return -1;
}
vector<vector<pii>> graph(n);
for(const auto & edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
graph[v].emplace_back(u, w);
}
priority_queue<pii, vector<pii>, greater<pii>> pq;
vector<int> distance(n, INT_MAX);
pq.emplace(0, 0);
distance[0] = 0;
while(!pq.empty()) {
const auto [dist, cur] = pq.top();
pq.pop();
if(dist > distance[cur]) continue;
for(const auto & [adj, w]: graph[cur]) {
if(distance[adj] > max(dist, w)) {
distance[adj] = max(dist, w);
pq.emplace(distance[adj], adj);
}
}
}
int ans = *max_element(distance.begin(), distance.end());
return ans == INT_MAX ? -1 : ans;
}
};
有点难。具体的做法还是比较容易想的,实际写起来会有一点问题。
- 首先还是套 dijkstra。
- 接着统计一下在限度内能够访问到的真正的节点。
- 最后统计超过阈值的边有多少能够访问。
- 计算{u,v}的访问情况。假设有 dist[u],dist[v], 所以左边的点能够继续访问 maxMove - dist[u], 右边的点能够访问 maxMove-dist[v]。很明显要保证非负数。
- 最后将两者相加,取边分裂节点和他的最小值即可。
C++
using pii = pair<int,int>;
class Solution {
public:
int reachableNodes(vector<vector<int>>& edges, int maxMoves, int n) {
vector<vector<pii>> graph(n);
for(const auto & edge: edges) {
int u = edge[0], v = edge[1], cost = edge[2] + 1; // move will be more than 1.
graph[u].emplace_back(v, cost);
graph[v].emplace_back(u, cost);
}
priority_queue<pii, vector<pii>, greater<pii>> pq;
pq.emplace(0, 0);
vector<int> distance(n, INT_MAX);
distance[0] = 0;
while(!pq.empty()) {
const auto [dist, cur] = pq.top();
pq.pop();
if(distance[cur] < dist) continue;
for(const auto & [adj, w]: graph[cur]) {
if(distance[adj] > dist + w) {
distance[adj] = dist + w;
pq.emplace(dist + w, adj);
}
}
}
int ans = 0;
for(const auto & dist: distance) {
if(dist <= maxMoves) ans++; // Calculate two endpoints.
}
for(const auto & edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
int u_dist = max(0, maxMoves - distance[u]);
int v_dist = max(0, maxMoves - distance[v]);
ans += min(u_dist + v_dist, w);
}
return ans;
}
};
明天打算开始不定期学一下 golang 了
要兑现自己说过的话 ![]()
如果有能力也想做一些 lab
p3 是哪里啊
图书馆——(旧)电院群楼的路上的桥上
悲![]()
回来吧我的电院()
2025 年 6 月 16 日 星期一 天气:多云/晴
X: @AlicitruSalt
今天是难得一见的好天气。所以上午就被要求写文档了。
先和学长再次确定了他们需要什么,面对节点故障,链路故障和多任务的情况下 ECMP 在两层 clos 数据中心中会怎么表现从而出现拥塞的情况。一上午就是画图/讨论/思考就结束了。
下午正式解决代码库的问题。我们面临的问题如下:
- 基于离散事件网络仿真工具 ns-3.18 开发。
- 当前代码采用 gcc-5/g+±5 才能运行,高于该版本的将会出错。而我也没有余力进行重构,这是一个痛苦的工作。
- 代码采用经典 makefile 模式,需要构造
compile_commands.json来支持 language server(这里采用 clangd)。 - vscode debug 无法进行。
于是首先:
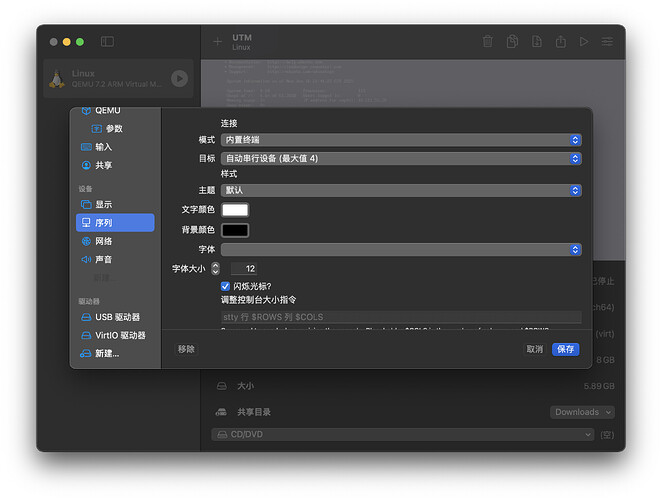
我们寻找到了 ubuntu 18.04 server 版虚拟机。鉴于我的电脑是 M1 芯片,因此选择 aarch64/arm64 版本安装在 UTM 上。(docker 太慢了并且远程调试目前无法解决,太菜 QAQ)
随后,UTM 的屏幕显示 No display available。无法通过屏幕进行任何操作,这是因为上古的 ubuntu 的 grub 引导程序不会从屏幕输出,需要我们新增加一个串行端口。新建一个串行端口即可。
随后我们只安装 openssh 服务器和必需的服务即可。这样就启动了。然后安装 gcc/g++ 5.5,gdb, make, bear,clangd-8 并且在 /usr/bin 创建软连接指向 gcc/g++/gdb/clangd即可。
随后采用 bear make 的方式来构建我们的项目,bear 将会自动追踪 makefile 过程生成我们需要的 compile_commands.json。将其作为 clangd 的参考文件提供给 language server 即可。
最后解决 debug 问题。我们构建文件后,只需要找到目标运行文件,将其作为 launch.json 的 program 的值即可。但是此时就会爆出错误:XXX_debug.so src file doesn’t exist。因此我们需要添加一些动态链接库,也就是给我们的 LD_LIBRARY_PATH. 我们只需要提供给环境系统 lib 和项目构建出来的 lib 即可。我们添加上:
{
"environment": [
{
"name": "PATH",
"value": "${workspaceFolder}/build/lib:${env:PATH}"
}
]
}
这样 debug 也就成功完成了。
晚上自然还是刷 leetcode 的。今天复习 floyd 算法后,明天就可以进入 bellman-ford 算法,prim-kruskal 算法的复习了。待图论大部分结束后,打算再转入 dp 和二分的复习。
前缀最小优化 O(n)。O(n^2) 当然可以。
C++
class Solution {
public:
int maximumDifference(vector<int>& nums) {
vector<int> prefix_min(nums.size(), INT_MAX);
prefix_min[0] = nums[0];
for(int i = 1; i < nums.size(); i++) {
prefix_min[i] = min(prefix_min[i-1], nums[i]);
}
int max_diff = -1;
for(int i = 1; i < nums.size(); i++) {
if(nums[i] == prefix_min[i-1]) continue;
max_diff = max(nums[i]-prefix_min[i-1], max_diff);
}
return max_diff;
}
};
Floyd 算法:最关键的就是遍历每个节点,随后判断将节点 k 塞入 u → v 的道路中是否会小于当前值。
for k = 0; k < n; k++ {
for i = 0; i < n; i++ {
for j = 0; j < n; j++ {
f[i][j] = min(f[i][j], f[i][k]+f[k][j]);
}
}
}
C++
class Solution {
public:
int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
vector<vector<int>> f(n, vector<int>(n, INT_MAX));
for(int i = 0; i < n; i++) {
f[i][i] = 0;
}
for(const auto & edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
f[u][v] = w;
f[v][u] = w;
}
for(int k = 0; k < n; k++) {
for(int u = 0; u < n; u++) {
if(f[u][k] == INT_MAX) continue; // Avoid overflow;
for(int v = 0; v < n; v++) {
if(f[k][v] == INT_MAX) continue;
f[u][v] = min(f[u][v], f[u][k] + f[k][v]);
}
}
}
vector<int> candidate(n, 0);
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(f[i][j] <= distanceThreshold) {
candidate[i]++;
}
}
}
int min_index = 0, min_city = INT_MAX;
for(int i = 0; i < n; i++) {
if(candidate[i] <= min_city) {
min_index = i;
min_city = candidate[i];
}
// cout << candidate[i] << ' ';
}
return min_index;
}
};
尝试一下静态数组吧。
C++
class Solution {
public:
long long minimumCost(string source, string target, vector<char>& original, vector<char>& changed, vector<int>& cost) {
using ll = long long;
ll f[26][26];
int n = 26;
for(int i = 0; i < n; i++) {
memset(f[i], 0x7f, sizeof(ll) * n);
f[i][i] = 0;
}
for(int i = 0; i < cost.size(); i++) {
ll u = original[i] - 'a', v = changed[i] - 'a', w = cost[i];
f[u][v] = min(w, f[u][v]);
}
for(int k = 0; k < n; k++) {
for(int i = 0; i < n; i++) {
if(f[i][k] == 0x7f7f7f7f7f7f7f7f) continue;
for(int j = 0; j < n; j++) {
if(f[k][j] == 0x7f7f7f7f7f7f7f7f) continue;
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}
}
}
ll ans = 0;
if(source.length() != target.length()) return -1;
for(int i = 0; i < source.length(); i++) {
int src = source[i] - 'a', tgt = target[i] - 'a';
ll cost = f[src][tgt];
if(cost == 0x7f7f7f7f7f7f7f7f) return -1;
ans += cost;
}
return ans;
}
};
需要枚举子集。枚举子集的方式就是从 i=0 → i=(1 << n), 判断某一个元素是否被取到可以有:i & (1 << k) 或者 (i >> k) & 1。
时间复杂度枚举 2^n 个子集,并做一次 floyd n^3. 也就是 O(2^n\times n^3). Floyd 算法需要 O(n^2) 空间。
C++
class Solution {
public:
int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
int **f = new int * [n];
int **graph = new int * [n];
// iterate over the subset.
for(int i = 0; i < n; i++) {
graph[i] = new int [n];
f[i] = new int [n];
memset(graph[i], 0x7f, sizeof(int) * n);
memset(f[i], 0x7f, sizeof(int) * n);
graph[i][i] = 0;
f[i][i] = 0;
}
for(const auto & edge: roads) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u][v] = min(w, graph[u][v]);
graph[v][u] = min(w, graph[v][u]);
}
int ans = 0;
for(int subset = 0; subset < (1 << n); subset++) {
// copy the viable f.
for(int i = 0; i < n; i++) {
if((subset >> i) & 1) {
for(int j = 0; j < n; j++) {
f[i][j] = graph[i][j];
}
}
}
for(int k = 0; k < n; k++) {
if(((subset >> k) & 1) == 0) continue;
for(int u = 0; u < n; u++) {
if(f[u][k] == 0x7f7f7f7f || ((subset >> u) & 1) == 0) continue;
for(int v = 0; v < n; v++) {
if(f[k][v] == 0x7f7f7f7f) continue;
f[u][v] = min(f[u][v], f[u][k] + f[k][v]);
}
}
}
bool flag = true;
for (int i = 0; i < n; i++) {
if (((subset >> i) & 1) == 0) continue;
for (int j = 0; j < i; j++) {
if ((subset >> j) & 1 && f[i][j] > maxDistance) {
flag = false;
break;
}
}
if(!flag) break;
}
if(!flag) continue;
ans += 1;
}
return ans;
}
};
今天就是这样了,又没有看 golang,该罚!!!, 大家晚安好梦~,明天上午 11 点二面,到时候再放一下面筋吧。