\displaystyle \int \dfrac{1+\cos{x}}{1+\sin^2{x}}~\mathrm{d}x
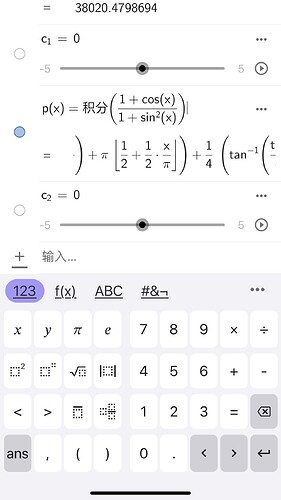
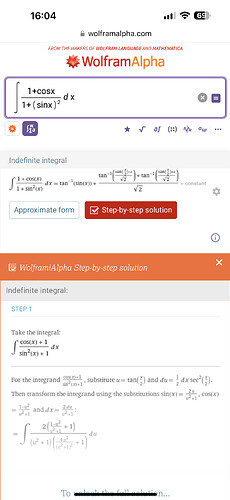
该不定积分如何计算?看了看 ggb 和 mathematica 的结果,有些复杂,不太像大一能写的
感谢门友相助,已解决(但是没找到“解决方案”按钮),下面梳理一下思路
- 取代换 t=\tan\left(\dfrac{x}{2}\right),得到一个有理函数的不定积分
- 对于分母中的二次三项式 x^2+px+q,可先配方得 \left(x+\dfrac{p}{2}\right)^2-\dfrac{p^2}{4}+q,再由平方差公式进一步化简,得到两个分式(打完才想起来 x 用过了,懒得改了)
- 最后查表并化简
最终结果(如果我没算错的话):\dfrac{\sqrt{2}\left(\sqrt{3+2\sqrt{2}}\arctan\left(\dfrac{\tan\dfrac{x}{2}}{\sqrt{3-2\sqrt{2}}}\right)-\sqrt{3-2\sqrt{2}}\arctan\left(\dfrac{\tan\dfrac{x}{2}}{\sqrt{3+2\sqrt{2}}}\right)\right)}{2}