算法做题记录

深入交流
42

核心就是数学归纳法（不仅限于自然数，也可以用于 dag 等结构）和反证法

1 Like
43

毕竟 recurrence 和 induction 是天作之合嘛 :smiling_face_with_3_hearts_people_hugging:

44

dag 上的数学归纳叫做拓扑排序，所有的 dp 都可以找到一个 dag 描述，dp 计算过程就是一种特殊的拓扑排序。

1 Like
45

DP 是拓扑排序这个没想出来，明天再看看 :magic_wand_brain:

46

就是 dp 的定义 状态设计就是计算图的节点 状态转移就是一种规定好的拓扑排序 要求无有效性就是要求计算图无环

例如 Dijkstra，s 到其余节点最短路。
已知 s 到所有节点的最短路是客观存在的
状态设计：节点 ai 代表离 s 第 i 近的边，a0 就是 s
状态转移：依据贝尔曼条件，s 到 ai 最短路是（遍历 s 到 aj 最短路 加 j 到 i 的边）的遍历最小值

这样的状态设计是有环的 s 到每个节点的最短路都依赖 s 到其他节点的最短路

dag：要求所有边是正边，这样 s 到 ai 的最短路就只需要考虑满足 j 小于 i 的 aj 了（正边条件砍掉了计算图里大概一半的边）

1 Like
47

typo：无后效性对应 dag

1 Like
48

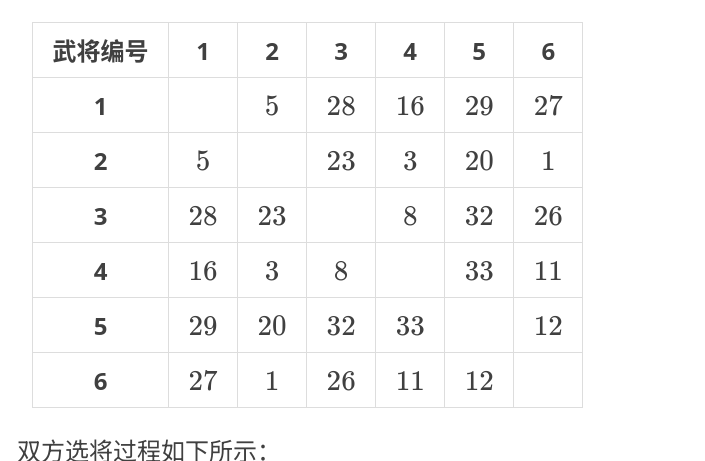
P1199 [NOIP2010 普及组] 三国游戏

过了！

我发现这个表格中每一行的最大值都绝对不会被任何一方拿到，所以 Alice 只要能拿到每一行的第二大的值中的最大的那个，就一定会赢，不存在会输的情况。

image
image705×461 13.3 KB

#include <iostream>
#include <vector>

using namespace std;

typedef long long ll;

void solve() {
    int n;
    cin >> n;

    vector<ll> largest(n);
    vector<ll> second_largest(n);

    for (int i = 0; i < n - 1; i++) {
        for (int j = i + 1; j < n; j++) {
            ll input;
            cin >> input;

            if (input > largest[i]) {
                second_largest[i] = largest[i];
                largest[i] = input;
            } else if (input > second_largest[i]) {
                second_largest[i] = input;
            }

            if (input > largest[j]) {
                second_largest[j] = largest[j];
                largest[j] = input;
            } else if (input > second_largest[j]) {
                second_largest[j] = input;
            }
        }
    }

    ll second_max = 0;
    for (ll sl : second_largest) {
        second_max = max(second_max, sl);
    }

    cout << "1" << endl;
    cout << second_max << endl;
}

int main() {
    ios::sync_with_stdio(false);

    solve();

    return 0;
}

特别开心的一集

1 Like